Venn diagrams are a powerful visual tool used in set theory, logic, statistics, and various fields of mathematics and science. They provide a clear and intuitive way to represent relationships between different sets, making complex ideas more accessible. This article will explore Venn diagrams in detail, including their definition, construction, types, applications, and illustrative explanations to enhance understanding.
1. Definition of a Venn Diagram
A Venn diagram is a graphical representation of sets and their relationships. It typically consists of overlapping circles, where each circle represents a set. The areas where the circles overlap indicate the elements that are common to the sets, while the areas that do not overlap represent elements that are unique to each set.
Illustrative Explanation:
Consider two sets, 
and 
:
- Let
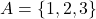
- Let
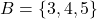
A Venn diagram for these sets would consist of two overlapping circles. The overlap represents the common element 
, while the non-overlapping parts represent the unique elements 
(in set ) and 
(in set ).
2. Construction of a Venn Diagram
To construct a Venn diagram, follow these steps:
A. Identify the Sets
Determine the sets you want to represent. For example, let’s consider three sets:
B. Draw the Circles
Draw circles for each set. For three sets, you will draw three overlapping circles. Label each circle with the corresponding set name.
C. Fill in the Elements
Place the elements in the appropriate regions of the diagram:
1. Common Elements: Place elements that are common to all sets in the overlapping area of all circles.
2. Unique Elements: Place elements that belong to only one set in the non-overlapping areas of the respective circles.
Illustrative Example:
For the sets , , and 
:
- The common element 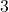goes in the center where all three circles overlap.
- The element
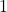goes in the part of circle that does not overlap with the others. - The element
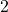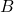goes in the overlapping area of circles and . - The element
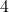goes in the overlapping area of circles 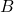and 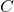. - The element
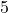goes in the part of circle 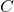that does not overlap with the others.
The completed Venn diagram would visually represent the relationships among the three sets.
3. Types of Venn Diagrams
Venn diagrams can represent various numbers of sets, and their complexity increases with the number of sets involved:
A. Two-Set Venn Diagrams
The simplest form, consisting of two overlapping circles. It is used to show relationships between two sets.
Illustrative Explanation:
For sets and :
The Venn diagram would show:
- Circle contains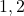
- Circle 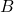contains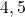
- The overlap contains
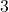
B. Three-Set Venn Diagrams
These diagrams consist of three overlapping circles and can represent more complex relationships.
Illustrative Explanation:
For sets , , and :
The Venn diagram would show:
- The overlap of all three circles contains .
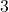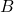- The overlap of and contains .
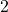- The overlap of 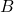and 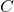contains .
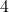- Unique elements 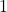and 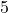are placed in their respective circles.
C. Multi-Set Venn Diagrams
Venn diagrams can also represent more than three sets, although they become increasingly complex and harder to interpret visually.
Illustrative Explanation:
For four sets 
, you would typically use a more complex arrangement of overlapping shapes, often requiring additional notation or color coding to distinguish between the various intersections.
4. Applications of Venn Diagrams
Venn diagrams have a wide range of applications across different fields:
A. Set Theory
Venn diagrams are primarily used in set theory to visualize relationships between sets, such as unions, intersections, and differences.
Illustrative Explanation:
- Union: The area covered by both circles represents the union of sets and 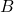, denoted as
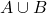. - Intersection: The overlapping area represents the intersection of sets and 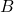, denoted as
. - Difference: The area of set that does not overlap with set 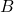represents the difference
.
B. Logic and Probability
In logic, Venn diagrams can illustrate logical relationships and help visualize the truth values of propositions. In probability, they can represent events and their probabilities.
Illustrative Explanation:
For example, if represents the event of rolling an even number on a die and represents the event of rolling a number greater than 3, the Venn diagram can show the probabilities of these events and their intersection.
C. Statistics
Venn diagrams are used in statistics to represent the relationships between different groups or categories of data.
Illustrative Explanation:
In a survey, if you want to analyze the preferences of a group of people for different types of music (e.g., rock, pop, jazz), a Venn diagram can help visualize how many people like multiple genres versus those who like only one.
D. Education
Venn diagrams are commonly used in educational settings to teach concepts of set theory, logic, and critical thinking.
Illustrative Explanation:
Teachers often use Venn diagrams to help students understand the relationships between different concepts, such as animals that are mammals, reptiles, or birds, allowing students to visually categorize and compare characteristics.
5. Conclusion
In summary, Venn diagrams are a versatile and effective tool for visualizing relationships between sets. They provide a clear and intuitive way to represent complex ideas, making them invaluable in mathematics, logic, statistics, and education. Understanding how to construct and interpret Venn diagrams enhances our ability to analyze relationships and draw conclusions based on set theory. Through illustrative explanations and examples, we can appreciate the significance of Venn diagrams in mathematical reasoning and their practical applications in real-world scenarios. As we continue to explore the world of mathematics and logic, Venn diagrams will remain a central concept, contributing to our understanding of relationships and enhancing our analytical skills. This understanding not only enriches our mathematical knowledge but also empowers us to apply these concepts in diverse disciplines, leading to innovative solutions and insights.