Vertical circular motion is a fascinating concept in physics that describes the motion of an object traveling in a circular path while subjected to gravitational forces. This type of motion is commonly observed in various real-world scenarios, such as amusement park rides, pendulums, and the motion of planets. This extensive article will delve into the definition of vertical circular motion, its characteristics, forces involved, equations of motion, examples, and applications, providing illustrative explanations for each concept.
Definition of Vertical Circular Motion
Vertical circular motion refers to the motion of an object that moves in a circular path while oriented vertically. Unlike horizontal circular motion, where the gravitational force acts perpendicular to the motion, in vertical circular motion, gravity acts in the same direction as the motion at certain points, affecting the object’s speed and acceleration.
Illustrative Explanation
Imagine a roller coaster that loops upside down. As the coaster travels along the vertical loop, it experiences changes in speed and direction due to the gravitational force acting on it. This scenario exemplifies vertical circular motion, where the coaster moves in a circular path while being influenced by gravity.
Characteristics of Vertical Circular Motion
Vertical circular motion has several key characteristics that define its behavior:
1. Centripetal Force: In vertical circular motion, a net inward force, known as centripetal force, is required to keep the object moving in a circular path. This force acts toward the center of the circular path.
Illustrative Explanation
Think of a child swinging a bucket of water in a vertical circle. The tension in the rope provides the centripetal force needed to keep the bucket moving in a circle. If the rope breaks, the bucket will fly off in a straight line due to inertia.
2. Gravitational Force: Gravity plays a crucial role in vertical circular motion. At different points in the circular path, the gravitational force affects the object’s speed and the required centripetal force.
Illustrative Explanation
Consider a pendulum swinging in a vertical circle. At the highest point of the swing, gravity acts downward, while at the lowest point, gravity acts against the motion. This variation in gravitational influence affects the pendulum’s speed and tension in the string.
3. Speed Variation: The speed of an object in vertical circular motion is not constant. It varies depending on the position of the object in the circular path. The object moves fastest at the lowest point and slowest at the highest point.
Illustrative Explanation
Imagine a ball being tossed in the air. As it rises, it slows down due to gravity until it reaches its highest point, where it momentarily stops before falling back down. Similarly, in vertical circular motion, the object speeds up and slows down as it moves through the circular path.
Forces Involved in Vertical Circular Motion
Several forces act on an object in vertical circular motion, including:
1. Centripetal Force (
): This is the net force required to keep the object moving in a circular path. It is directed toward the center of the circle and is given by the formula:
![\[ F_c = \frac{mv^2}{r} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-ddbe1ef8dbbae887a22d84fae51ef6e3_l3.png "Rendered by QuickLaTeX.com")
Where:
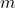is the mass of the object.
is the tangential speed of the object.
is the radius of the circular path.
Illustrative Explanation
Picture a car turning around a curve. The friction between the tires and the road provides the centripetal force needed to keep the car on the curved path. If the speed is too high or the curve is too sharp, the car may skid off the road.
2. Gravitational Force (
): The gravitational force acting on the object is given by:
![\[ F_g = mg \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-d5ee882fb3532b0aea232d93f868e526_l3.png "Rendered by QuickLaTeX.com")
Where:
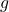is the acceleration due to gravity (approximately 
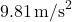on Earth).
Illustrative Explanation
Imagine holding a ball in your hand. The weight of the ball (gravitational force) pulls it downward. In vertical circular motion, this force influences the object’s speed and the tension in the supporting string or rod.
3. Tension Force (
): In cases where the object is attached to a string or rod (like a pendulum or a roller coaster), the tension in the string or rod provides additional force to maintain circular motion.
Illustrative Explanation
Think of a swing at a playground. As you push the swing, the tension in the chains helps keep the swing moving in a circular path. If you stop pushing, the swing will slow down and eventually stop due to gravity.
Equations of Motion in Vertical Circular Motion
The motion of an object in vertical circular motion can be described using several key equations:
1. At the Highest Point: At the highest point of the circular path, the centripetal force is provided by the gravitational force and the tension in the string (if applicable). The equation can be expressed as:
![\[ T + mg = \frac{mv^2}{r} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-7343f230b137d0ef86e8f7554e4b4c93_l3.png "Rendered by QuickLaTeX.com")
Where is the tension in the string.
Illustrative Explanation
Imagine a roller coaster at the top of a loop. The gravitational force pulls the coaster down, while the tension in the track helps keep it on the circular path. The combination of these forces determines the coaster’s speed at the highest point.
2. At the Lowest Point: At the lowest point, the centripetal force is provided by the tension in the string and the gravitational force acting downward:
![\[ T - mg = \frac{mv^2}{r} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-f6d0478b5441be47b88a2c9106d3a254_l3.png "Rendered by QuickLaTeX.com")
Illustrative Explanation
Picture a pendulum swinging down to its lowest point. The tension in the string must be greater than the gravitational force to keep the pendulum moving in a circular path. If the tension is insufficient, the pendulum will not complete the swing.
3. Conservation of Energy: The total mechanical energy of the object in vertical circular motion is conserved (assuming no energy losses due to friction or air resistance). The potential energy and kinetic energy can be expressed as:
![\[ KE + PE = \text{constant} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-6d544fb00a4809607c5c8d734da00fe5_l3.png "Rendered by QuickLaTeX.com")
Where:
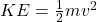(kinetic energy)
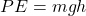(potential energy, where 
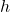is the height above a reference point)
Illustrative Explanation
Think of a swing at a playground. When the swing is at its highest point, it has maximum potential energy and minimum kinetic energy. As it swings down, potential energy converts to kinetic energy, allowing the swing to move faster.
Examples of Vertical Circular Motion
Vertical circular motion can be observed in various real-world scenarios:
1. Amusement Park Rides: Roller coasters often feature loops and drops that exemplify vertical circular motion. Riders experience changes in speed and forces as they navigate the circular paths.
Illustrative Explanation
Imagine riding a roller coaster that goes through a vertical loop. At the top of the loop, you feel lighter due to the combination of gravitational and centripetal forces. As you descend, you feel heavier as the forces change.
2. Pendulums: A pendulum swinging in a vertical circle demonstrates vertical circular motion. The gravitational force affects the pendulum’s speed and tension in the string as it swings.
Illustrative Explanation
Picture a grandfather clock with a swinging pendulum. As the pendulum swings back and forth, it moves in a circular path, with gravity influencing its speed and direction.
3. Planetary Motion: The motion of planets around the sun can be approximated as vertical circular motion, where gravitational forces act as the centripetal force keeping the planets in orbit.
Illustrative Explanation
Think of the Earth orbiting the sun. The gravitational pull from the sun acts as the centripetal force, keeping the Earth in a circular path around it.
Applications of Vertical Circular Motion
Vertical circular motion has numerous applications across various fields:
1. Engineering: Understanding vertical circular motion is crucial in designing amusement park rides, roller coasters, and other structures that involve circular motion.
Illustrative Explanation
Engineers must calculate the forces acting on a roller coaster to ensure it is safe and enjoyable for riders. They consider the effects of gravity, speed, and tension in the design process.
2. Physics Education: Vertical circular motion is a common topic in physics courses, helping students understand concepts such as centripetal force, energy conservation, and the effects of gravity.
Illustrative Explanation
In a physics lab, students may conduct experiments to observe vertical circular motion using pendulums or rotating systems, reinforcing their understanding of the principles involved.
3. Sports: Athletes in sports such as gymnastics and diving experience vertical circular motion during their routines, where they must control their speed and orientation while in the air.
Illustrative Explanation
Think of a diver performing a somersault off a diving board. As they rotate in the air, they experience vertical circular motion, requiring precise control to enter the water safely.
Conclusion
In conclusion, vertical circular motion is a fundamental concept in physics characterized by the motion of an object traveling in a circular path while influenced by gravitational forces. Understanding the characteristics, forces involved, equations of motion, and applications of vertical circular motion is essential for grasping various physical phenomena. From amusement park rides to planetary motion, vertical circular motion plays a vital role in our understanding of the natural world and engineering applications. By appreciating the intricacies of vertical circular motion, we can better navigate its implications in both scientific and everyday contexts.