Cara Menghitung Percepatan Sentripetal pada Roda Gigi

Fisika

Percepatan sentripetal adalah percepatan yang dialami oleh suatu objek yang bergerak dalam lintasan melingkar. Dalam konteks roda gigi, percepatan sentripetal sangat penting untuk memahami bagaimana gaya bekerja pada bagian-bagian yang berputar. Roda gigi digunakan dalam berbagai aplikasi mekanis, mulai dari mesin sederhana hingga sistem kompleks dalam otomotif dan industri. Artikel ini akan membahas secara mendetail tentang apa itu percepatan sentripetal, bagaimana cara menghitungnya pada roda gigi, serta langkah-langkah dan contoh perhitungan yang relevan.

1. Pengertian Percepatan Sentripetal

a. Definisi Percepatan Sentripetal

Percepatan sentripetal adalah percepatan yang diperlukan untuk menjaga suatu objek tetap bergerak dalam lintasan melingkar. Percepatan ini selalu mengarah ke pusat lingkaran dan berfungsi untuk mengubah arah gerakan objek, meskipun kecepatan liniernya tetap konstan. Percepatan sentripetal (a_c) dapat dihitung dengan rumus:

    \[ a_c = \frac{v^2}{r} \]

Di mana:

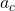  • a_c = percepatan sentripetal (dalam meter per detik kuadrat, m/s²)
  • v = kecepatan linier objek (dalam meter per detik, m/s)
  • r = jari-jari lintasan melingkar (dalam meter, m)

b. Pentingnya Percepatan Sentripetal

Memahami percepatan sentripetal sangat penting dalam desain dan analisis sistem mekanis, termasuk roda gigi. Dalam roda gigi, percepatan sentripetal membantu menentukan gaya yang diperlukan untuk menjaga agar gigi tetap berputar dengan stabil dan efisien.

2. Menghitung Percepatan Sentripetal pada Roda Gigi

Untuk menghitung percepatan sentripetal pada roda gigi, kita perlu mengetahui dua parameter utama: kecepatan linier roda gigi dan jari-jari lingkaran yang dilalui oleh titik pada tepi roda gigi. Berikut adalah langkah-langkah untuk menghitung percepatan sentripetal:

a. Menentukan Jari-jari Roda Gigi

Jari-jari roda gigi (r) adalah jarak dari pusat roda gigi ke tepi luar gigi. Jari-jari ini dapat diukur secara langsung atau dihitung berdasarkan diameter roda gigi. Jika diameter roda gigi diketahui, jari-jari dapat dihitung dengan rumus:

    \[ r = \frac{d}{2} \]

Di mana:

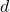  • d = diameter roda gigi (dalam meter)

b. Menentukan Kecepatan Linier

Kecepatan linier (v) pada tepi roda gigi dapat dihitung berdasarkan kecepatan sudut (\omega) roda gigi. Kecepatan sudut diukur dalam radian per detik (rad/s) dan dapat dihitung dengan rumus:

    \[ v = r \cdot \omega \]

c. Menghitung Percepatan Sentripetal

Setelah mendapatkan nilai jari-jari dan kecepatan linier, kita dapat menghitung percepatan sentripetal menggunakan rumus yang telah disebutkan sebelumnya:

    \[ a_c = \frac{v^2}{r} \]

3. Contoh Perhitungan Percepatan Sentripetal pada Roda Gigi

Mari kita lihat contoh perhitungan untuk lebih memahami cara menghitung percepatan sentripetal pada roda gigi.

Contoh Kasus

Misalkan kita memiliki roda gigi dengan diameter 0,5 meter dan berputar dengan kecepatan sudut 10 rad/s. Kita ingin menghitung percepatan sentripetal pada tepi roda gigi.

Langkah 1: Menghitung Jari-jari Roda Gigi

Pertama, kita hitung jari-jari roda gigi:

    \[ r = \frac{d}{2} = \frac{0,5 \, \text{m}}{2} = 0,25 \, \text{m} \]

Langkah 2: Menghitung Kecepatan Linier

Selanjutnya, kita hitung kecepatan linier:

    \[ v = r \cdot \omega = 0,25 \, \text{m} \cdot 10 \, \text{rad/s} = 2,5 \, \text{m/s} \]

Langkah 3: Menghitung Percepatan Sentripetal

Sekarang kita dapat menghitung percepatan sentripetal:

    \[ a_c = \frac{v^2}{r} = \frac{(2,5 \, \text{m/s})^2}{0,25 \, \text{m}} = \frac{6,25 \, \text{m}^2/\text{s}^2}{0,25 \, \text{m}} = 25 \, \text{m/s}^2 \]

Jadi, percepatan sentripetal pada tepi roda gigi adalah 25 m/s².

4. Kesimpulan

Percepatan sentripetal adalah konsep penting dalam fisika yang menjelaskan bagaimana objek bergerak dalam lintasan melingkar. Dalam konteks roda gigi, menghitung percepatan sentripetal membantu kita memahami gaya yang bekerja pada sistem dan memastikan bahwa roda gigi beroperasi dengan efisien dan stabil. Dengan mengikuti langkah-langkah yang telah dijelaskan, kita dapat dengan mudah menghitung percepatan sentripetal berdasarkan jari-jari dan kecepatan linier. Pengetahuan ini sangat berguna dalam desain dan analisis sistem mekanis, serta dalam berbagai aplikasi teknik dan industri.