Perpindahan dan Jarak untuk Pemahaman Lebih Baik

Perpindahan dan jarak adalah konsep mendasar dalam fisika yang sering kali membingungkan. Keduanya memiliki peran penting dalam memahami gerak suatu benda, tetapi memiliki makna dan implikasi yang berbeda. Artikel ini akan menjelaskan secara rinci kedua konsep tersebut, memberikan contoh nyata, dan menjawab pertanyaan umum untuk memperdalam pemahaman Anda.

Section 1: Pengertian Perpindahan dan Jarak

Definisi Dasar

Perpindahan dan jarak adalah dua konsep yang mendasar dalam fisika, terutama dalam kajian kinematika yang berkaitan dengan gerak. Meskipun sering dianggap serupa, perpindahan dan jarak memiliki perbedaan mendasar baik dalam pengertian fisik maupun matematis.

Jarak adalah panjang total lintasan yang ditempuh oleh sebuah benda saat bergerak dari satu titik ke titik lain, tanpa memperhatikan arah gerak. Jarak selalu bernilai positif dan merupakan besaran skalar, yang hanya memuat informasi tentang “berapa jauh”.
Perpindahan, di sisi lain, adalah perubahan posisi benda dari titik awal ke titik akhir. Perpindahan adalah besaran vektor yang memiliki nilai (magnitude) dan arah. Nilai perpindahan bisa positif, negatif, atau nol tergantung pada perubahan posisi benda.

Ilustrasi Perbedaan

Bayangkan seseorang berjalan mengelilingi lapangan berbentuk persegi panjang. Jika ia memulai perjalanan dari sudut A, berjalan sepanjang sisi-sisi lapangan, dan kembali ke titik A, jarak yang ditempuh adalah total panjang semua sisi yang dilalui. Namun, perpindahan orang tersebut adalah nol karena posisi awal dan akhirnya sama.

Satuan dalam SI

Baik jarak maupun perpindahan diukur dalam meter (m) dalam Sistem Internasional (SI). Dalam beberapa kasus, kilometer (km), sentimeter (cm), atau satuan lain digunakan untuk mempermudah perhitungan praktis.

Aplikasi dalam Kehidupan Sehari-hari

Konsep perpindahan dan jarak digunakan dalam berbagai aspek kehidupan, seperti:
1. Navigasi: Dalam aplikasi GPS, jarak menunjukkan total lintasan yang harus dilalui, sementara perpindahan memberikan garis lurus dari posisi awal ke tujuan.
2. Olahraga: Dalam balapan, jarak yang ditempuh mengukur usaha total, tetapi perpindahan menentukan seberapa jauh dari titik awal seorang pelari telah bergerak.

Section 2: Perbedaan Konseptual dan Matematika antara Perpindahan dan Jarak

Analisis Detail Perbedaan

Untuk lebih memahami perbedaan mendalam antara jarak dan perpindahan, kita perlu menggali konsep fisik dan matematisnya.

1. Sifat Skalar vs. Vektor
– Jarak adalah besaran skalar, sehingga hanya memiliki nilai tanpa arah. Misalnya, jika seseorang bergerak 5 meter ke utara, lalu 5 meter ke selatan, jarak totalnya adalah 10 meter.
– Perpindahan adalah besaran vektor yang dipengaruhi oleh arah. Dalam contoh yang sama, perpindahan hanya 0 meter karena posisi akhir dan awal sama.

2. Persamaan Matematika
– Jarak (s):

$s = \sum |d_i|$

Di mana $d_i$ adalah setiap segmen kecil lintasan yang ditempuh oleh benda. Jarak selalu positif.

– Perpindahan ( $\Delta x$ ):

$\Delta x = x_{\text{akhir}} - x_{\text{awal}}$

Di mana $x_{\text{akhir}}$ adalah posisi akhir, dan $x_{\text{awal}}$ adalah posisi awal. Perpindahan memperhitungkan perubahan posisi secara langsung, termasuk arah.

3. Hubungan dengan Grafik Gerak
– Pada grafik posisi-waktu, jarak adalah panjang seluruh lintasan pada sumbu vertikal yang dilalui oleh kurva grafik.
– Perpindahan adalah jarak vertikal antara titik awal dan akhir kurva pada grafik posisi-waktu.

4. Contoh Numerik
– Kasus 1: Seseorang bergerak 4 meter ke timur, lalu 3 meter ke barat.
– Jarak: $4 + 3 = 7 \, \text{meter}$
– Perpindahan: $4 - 3 = 1 \, \text{meter ke timur}$ .

– Kasus 2: Sebuah mobil mengelilingi lintasan melingkar sejauh 100 meter dan kembali ke posisi awal.
– Jarak: $100 \, \text{meter}$ .
– Perpindahan: $0 \, \text{meter}$ , karena posisi awal dan akhirnya sama.

Representasi dalam Sistem Koordinat

Dalam sistem koordinat kartesius (2D atau 3D), perpindahan dihitung dengan menggunakan teorema Pythagoras. Jika posisi awal adalah $(x_1, y_1)$ dan posisi akhir adalah $(x_2, y_2)$ :

$\Delta r = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$

Sementara jarak tergantung pada panjang lintasan yang ditempuh, yang mungkin melibatkan beberapa segmen lintasan melengkung atau zig-zag.

Hubungan dengan Kecepatan

Jarak berkaitan dengan kecepatan skalar rata-rata ( $v_{\text{avg}}$ ):

$v_{\text{avg}} = \frac{\text{jarak}}{\text{waktu}}$

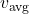Perpindahan berkaitan dengan kecepatan rata-rata ( $\vec{v}_{\text{avg}}$ ):

$\vec{v}_{\text{avg}} = \frac{\text{perpindahan}}{\text{waktu}}$

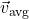Aplikasi dalam Perhitungan

Dalam desain transportasi, seperti rel kereta api, jarak menentukan bahan yang diperlukan untuk membangun jalur, sementara perpindahan menunjukkan efisiensi jalur tersebut.
Dalam analisis gerak astronomi, perpindahan digunakan untuk menghitung orbit, sementara jarak membantu menentukan panjang lintasan.

Section 3: Implementasi Perpindahan dan Jarak dalam Berbagai Skenario

1. Penerapan dalam Fisika dan Teknik

Konsep perpindahan dan jarak tidak hanya penting dalam teori, tetapi juga dalam aplikasi praktis. Berikut adalah beberapa bidang di mana keduanya sangat relevan:

A. Kinematika di Dunia Nyata

Dalam studi gerak benda:

Jarak digunakan untuk menghitung lintasan yang dilalui oleh kendaraan, satelit, atau objek lainnya tanpa mempertimbangkan perubahan arah.
Perpindahan digunakan untuk analisis posisi benda relatif terhadap titik awalnya. Hal ini penting untuk memahami gerak dalam sistem koordinat dan memprediksi lintasan.

Contoh: Peluncuran roket ke luar angkasa melibatkan kalkulasi perpindahan untuk mencapai orbit tertentu, sementara jarak menunjukkan panjang total perjalanan.

B. Teknik Sipil

Dalam merancang jalan raya, jembatan, atau rel kereta api, jarak membantu menentukan bahan yang diperlukan. Sementara itu, perpindahan membantu merancang struktur yang efisien dengan menentukan lokasi akhir relatif terhadap lokasi awal.

2. Studi Kasus Gerak Lurus dan Gerak Melingkar

Gerak Lurus

Jika sebuah mobil bergerak dari titik A ke B sejauh 5 meter ke timur dan kemudian 5 meter ke barat:

– Jarak: $5 + 5 = 10 \, \text{meter}$ .
– Perpindahan: $0 \, \text{meter}$ (karena posisi awal dan akhir sama).

Gerak Melingkar

Dalam gerak melingkar, seperti sebuah mobil yang bergerak mengelilingi lintasan lingkaran dengan jari-jari $r = 10 \, \text{meter}$ :

Jarak dalam satu putaran penuh adalah keliling lingkaran:

$s = 2 \pi r = 2 \pi (10) = 62.8 \, \text{meter}$

Perpindahan dalam satu putaran penuh adalah nol karena posisi awal dan akhir sama.

3. Hubungan dengan Energi dan Usaha

Energi kinetik dan usaha seringkali bergantung pada perpindahan. Usaha ( $W$ ) dirumuskan sebagai:

$W = \vec{F} \cdot \vec{d}$

Jika gaya ( $\vec{F}$ ) dan perpindahan ( $\vec{d}$ ) searah, maka usaha bernilai positif. Jika tidak, usaha menjadi nol atau negatif. Jarak, dalam hal ini, tidak relevan karena arah tidak dipertimbangkan.

4. Aplikasi dalam Navigasi Modern

Sistem Navigasi GPS: GPS menghitung jarak total untuk memberikan estimasi waktu tempuh, tetapi perpindahan digunakan untuk memberikan arah langsung ke tujuan.
Robotika: Dalam robotika, algoritma navigasi membutuhkan perpindahan untuk memastikan robot mencapai titik tujuan dengan jalur optimal, sementara jarak digunakan untuk melacak total energi yang digunakan.

5. Simulasi dan Pengukuran di Lab

Dalam laboratorium fisika:

Jarak diukur menggunakan odometer atau pita pengukur.
Perpindahan dihitung menggunakan sensor posisi atau metode triangulasi berbasis laser.

6. Visualisasi Grafik

Dalam analisis grafik:

Pada grafik posisi-waktu, jarak adalah total panjang lintasan yang ditampilkan oleh kurva grafik, sedangkan perpindahan adalah jarak antara titik awal dan titik akhir pada sumbu vertikal grafik.
Dalam grafik kecepatan-waktu, luas di bawah kurva mencerminkan jarak jika semua nilai kecepatan positif, dan perpindahan jika kecepatan memiliki nilai positif dan negatif.

Kesimpulan

Pemahaman perpindahan dan jarak membantu menjelaskan berbagai fenomena dalam fisika dan teknik. Kedua konsep ini saling melengkapi, tergantung pada apakah analisis membutuhkan nilai total (jarak) atau efisiensi langsung (perpindahan). Keduanya tetap menjadi dasar dari banyak perhitungan praktis yang memengaruhi teknologi modern dan ilmu pengetahuan.

Tahun cahaya – Konsep, contoh jarak dan satuan lainnya

Mars (planet) – Informasi, struktur, karakteristik, misi

Sabuk Asteroid – Konsep, asal usul dan jarak

Mesin uap – Konsep, sejarah, kepentingan dan banyak lagi…

Konsep Usaha (dalam fisika) – Apa itu usaha, daya, dan banyak lagi