Vektor adalah objek matematika yang sangat penting dalam berbagai bidang ilmu pengetahuan, seperti fisika, matematika, teknik, dan ilmu komputer. Berbeda dengan skalar yang hanya memiliki besar (nilai), vektor memiliki dua atribut utama: besar (magnitude) dan arah. Misalnya, dalam fisika, kecepatan adalah vektor karena tidak hanya memiliki nilai (seberapa cepat suatu objek bergerak), tetapi juga ke mana arah gerak tersebut.
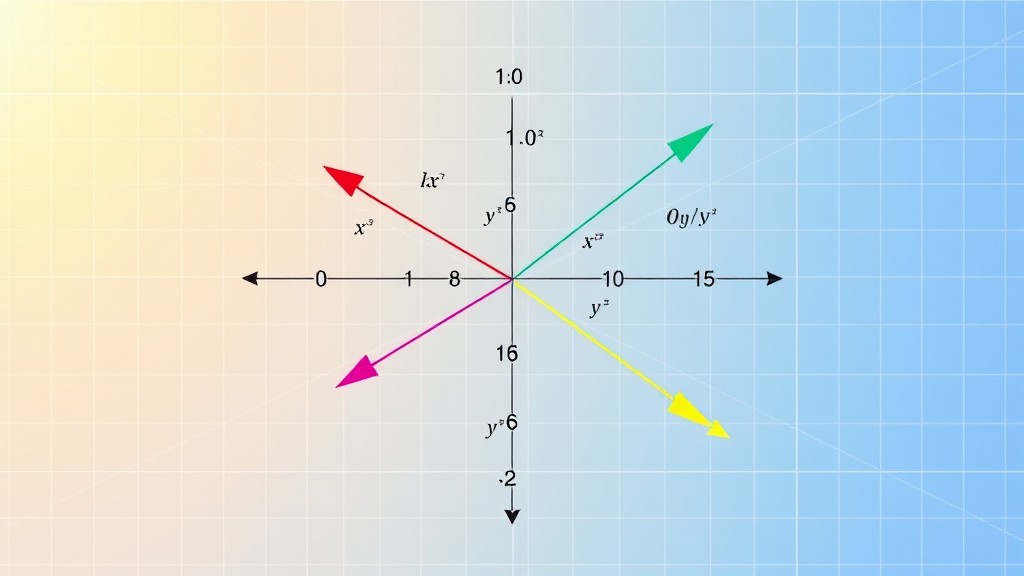
Pada artikel ini, kita akan membahas sifat-sifat dasar dari vektor, termasuk operasi-operasi yang dapat dilakukan dengan vektor, serta memberikan contoh ilustrasi untuk membantu memahami konsep-konsep ini dengan lebih baik.
Pengertian Vektor
Vektor adalah konsep fundamental dalam matematika dan fisika yang digunakan untuk mewakili besaran yang memiliki arah dan panjang (atau magnitudo). Vektor sangat berguna dalam menggambarkan banyak hal, seperti posisi, kecepatan, percepatan, dan gaya. Dalam matematika, vektor direpresentasikan oleh sebuah panah yang memiliki dua elemen utama: panjang (magnitude) dan arah.
Sebuah vektor dalam ruang dua dimensi biasanya diwakili oleh sebuah panah pada bidang datar, di mana panjang panah menunjukkan besar (magnitude) vektor, dan arah panah menunjukkan arah vektor. Dalam ruang tiga dimensi, vektor dapat direpresentasikan sebagai entitas geometris yang memiliki komponen dalam tiga sumbu (x, y, dan z).
Sebagai contoh, jika kita menganggap sebuah vektor yang menyatakan perpindahan, perpindahan tidak hanya menyangkut seberapa jauh suatu objek bergerak, tetapi juga ke arah mana objek tersebut bergerak. Jika Anda berjalan 5 meter ke utara, perpindahan Anda bisa direpresentasikan sebagai sebuah vektor dengan besar 5 meter dan arah ke utara.
Sebelum masuk ke sifat-sifat vektor, penting untuk memahami konsep dasar dari vektor itu sendiri. Vektor adalah besaran yang memiliki dua karakteristik:
- Panjang (Magnitude): Panjang atau besarnya vektor menunjukkan seberapa besar nilai dari vektor tersebut.
- Arah: Arah vektor menunjukkan ke mana vektor tersebut “mengarah” dalam ruang. Arah biasanya digambarkan dengan panah pada vektor.
Jika suatu besaran hanya memiliki panjang tetapi tidak memiliki arah (seperti suhu atau massa), maka besaran tersebut disebut skalar, bukan vektor.
Ilustrasi: Bayangkan vektor seperti panah. Panjang panah menunjukkan seberapa kuat atau besar besaran itu, sementara arah panah menunjukkan ke mana besaran itu bekerja. Misalnya, jika kita memiliki vektor gaya, panjang panah bisa mewakili besar gaya, dan arah panah mewakili arah gaya tersebut.
Sifat-Sifat Dasar Vektor
1. Penjumlahan Vektor
Penjumlahan vektor adalah salah satu operasi dasar yang bisa dilakukan dengan vektor. Jika kita memiliki dua vektor, hasil penjumlahan mereka adalah vektor baru yang disebut resultan. Penjumlahan vektor bisa dilakukan dengan menggunakan metode grafis atau metode aljabar.
Secara geometris, penjumlahan vektor dilakukan dengan metode segitiga atau metode paralelogram. Dalam metode segitiga, kita menempatkan ujung vektor pertama di pangkal vektor kedua, kemudian vektor resultan adalah vektor yang menghubungkan pangkal vektor pertama dengan ujung vektor kedua.
Ilustrasi: Bayangkan menambahkan dua gaya dengan cara meletakkan ujung panah satu vektor pada pangkal panah vektor lainnya. Hasil dari penjumlahan ini adalah vektor baru yang menunjukkan arah dan besaran gabungan dari dua gaya tersebut.
Contoh Penjumlahan Vektor:
Misalkan kita memiliki dua vektor A dan B. Jika kita menjumlahkan kedua vektor ini, kita dapat menggambarkan hasilnya seperti berikut:
A ------> B --------> Resultan: AB ---------------->
Di sini, Anda melihat bahwa kita menghubungkan ujung vektor A dengan pangkal vektor B, dan vektor resultan adalah garis lurus yang menghubungkan pangkal A dengan ujung B.
Secara matematis, jika vektor A memiliki komponen ![]() dan vektor B memiliki komponen
dan vektor B memiliki komponen ![]() , maka penjumlahan kedua vektor tersebut adalah vektor baru C dengan komponen:
, maka penjumlahan kedua vektor tersebut adalah vektor baru C dengan komponen:
![]()
Sifat Komutatif dan Asosiatif pada Penjumlahan Vektor
- Komutatif: Penjumlahan vektor adalah komutatif, artinya urutan penjumlahan tidak mempengaruhi hasil. Misalnya, jika kita memiliki vektor
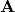 dan
dan 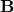 , maka
, maka 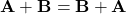 .
. - Asosiatif: Penjumlahan vektor juga asosiatif, yaitu
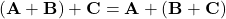 .
.
2. Pengurangan Vektor
Pengurangan vektor pada dasarnya adalah penjumlahan vektor dengan vektor negatif. Untuk mengurangkan dua vektor, kita cukup menjumlahkan vektor pertama dengan negasi dari vektor kedua. Negasi sebuah vektor adalah vektor yang memiliki besar yang sama tetapi arah yang berlawanan.
Ilustrasi: Pengurangan vektor seperti menarik benda ke dua arah yang berlawanan. Jika dua gaya bekerja dalam arah berlawanan, pengurangan keduanya akan menghasilkan vektor yang arahnya ke arah gaya yang lebih kuat, dengan panjang yang sesuai dengan selisih besar kedua gaya.
Contoh Pengurangan Vektor:
Misalkan kita ingin mengurangkan vektor B dari vektor A. Pertama-tama, kita menggambar negasi dari vektor B, yaitu vektor yang memiliki arah berlawanan dengan B. Kemudian, kita menjumlahkan A dengan vektor negatif dari B.
A ------> -B <-------- Resultan: A ------> <---------
Secara matematis, jika vektor A memiliki komponen ![]() dan vektor B memiliki komponen
dan vektor B memiliki komponen ![]() , maka pengurangan kedua vektor tersebut adalah vektor baru C dengan komponen:
, maka pengurangan kedua vektor tersebut adalah vektor baru C dengan komponen:
![]()
3. Perkalian Skalar dengan Vektor
Perkalian skalar adalah operasi di mana kita mengalikan sebuah vektor dengan sebuah bilangan skalar (nilai). Hasilnya adalah vektor baru yang searah atau berlawanan arah dengan vektor asli, tetapi dengan besar yang berbeda. Jika skalarnya positif, vektor hasil perkalian akan searah, tetapi jika skalarnya negatif, arah vektor akan berlawanan.
Ilustrasi: Jika kita memiliki gaya sebesar 10 Newton ke arah kanan dan mengalikannya dengan skalar 2, hasilnya adalah gaya 20 Newton ke arah yang sama. Jika kita mengalikannya dengan -1, arah gaya akan berbalik tetapi tetap dengan panjang yang sama.
Contoh Perkalian Skalar:
Misalkan kita memiliki vektor A dan ingin mengalikannya dengan skalar 2. Vektor hasil akan memiliki arah yang sama dengan A, tetapi panjangnya dua kali lipat.
A ------> 2A ------------------>
Jika kita mengalikan dengan skalar negatif, misalnya -1, maka arah vektor akan berbalik.
A ------> -1A <------
Secara matematis, jika vektor A memiliki komponen ![]() , maka perkalian skalar
, maka perkalian skalar ![]() dengan vektor A menghasilkan vektor baru B dengan komponen:
dengan vektor A menghasilkan vektor baru B dengan komponen:
![]()
4. Besarnya Vektor (Magnitude)
Besarnya vektor, atau magnitude, adalah panjang dari vektor dan biasanya dilambangkan dengan simbol ![]() . Dalam ruang dua dimensi, besar sebuah vektor A dengan komponen
. Dalam ruang dua dimensi, besar sebuah vektor A dengan komponen ![]() dan
dan ![]() dapat dihitung menggunakan teorema Pythagoras.
dapat dihitung menggunakan teorema Pythagoras.
![]()
Ilustrasi Besarnya Vektor:
Misalkan kita memiliki vektor A yang bergerak dalam ruang dua dimensi dengan komponen ![]() dan
dan ![]() . Maka besarnya vektor A adalah:
. Maka besarnya vektor A adalah:
![]()
Ilustrasi ini menunjukkan bahwa perpindahan dengan komponen 3 satuan ke kanan dan 4 satuan ke atas menghasilkan perpindahan total sepanjang 5 satuan.
5. Vektor Nol
Vektor nol adalah vektor yang memiliki besar 0 dan tidak memiliki arah tertentu. Vektor nol dilambangkan dengan ![]() . Vektor ini penting dalam operasi penjumlahan dan pengurangan, karena menambahkan vektor nol ke vektor lain tidak mengubah vektor tersebut.
. Vektor ini penting dalam operasi penjumlahan dan pengurangan, karena menambahkan vektor nol ke vektor lain tidak mengubah vektor tersebut.
Ilustrasi Vektor Nol:
Jika Anda menambahkan vektor A dengan vektor nol, hasilnya akan tetap vektor A. Vektor nol tidak mengubah besar atau arah vektor lain.
A + 0 = A
6. Perkalian Vektor dengan Vektor (Dot Product)
Dot product atau perkalian titik adalah operasi yang menghasilkan skalar dari dua vektor. Dot product didefinisikan sebagai:
![]()
di mana ![]() adalah sudut antara kedua vektor. Dot product digunakan untuk menghitung seberapa besar dua vektor sejalan satu sama lain. Jika sudut antara dua vektor adalah 0 derajat (vektor searah), dot product bernilai maksimum. Jika sudutnya 90 derajat (vektor tegak lurus), dot product bernilai nol.
adalah sudut antara kedua vektor. Dot product digunakan untuk menghitung seberapa besar dua vektor sejalan satu sama lain. Jika sudut antara dua vektor adalah 0 derajat (vektor searah), dot product bernilai maksimum. Jika sudutnya 90 derajat (vektor tegak lurus), dot product bernilai nol.
Ilustrasi: Dot product seperti menghitung seberapa besar gaya yang bekerja sepanjang arah tertentu. Jika kita mendorong benda sejajar dengan arah geraknya, dot product menghasilkan nilai maksimum. Namun, jika kita mendorong tegak lurus terhadap gerakan, tidak ada kerja yang dilakukan.
Contoh Dot Product:
Misalkan kita memiliki dua vektor A dan B yang membentuk sudut ![]() . Kita dapat menggunakan dot product untuk menghitung seberapa besar komponen vektor A searah dengan B.
. Kita dapat menggunakan dot product untuk menghitung seberapa besar komponen vektor A searah dengan B.
Jika besar vektor A adalah 5 dan besar vektor B adalah 4, maka dot product mereka adalah:
![]()
Ini berarti ada komponen vektor A sebesar 17.32 searah dengan B.
7. Perkalian Vektor dengan Vektor (Cross Product)
Cross product atau perkalian silang adalah operasi yang menghasilkan vektor baru yang tegak lurus terhadap kedua vektor awal. Cross product hanya berlaku dalam ruang tiga dimensi dan didefinisikan sebagai:
![]()
di mana ![]() adalah vektor satuan yang tegak lurus terhadap bidang yang dibentuk oleh A dan B, dan
adalah vektor satuan yang tegak lurus terhadap bidang yang dibentuk oleh A dan B, dan ![]() adalah sudut antara kedua vektor.
adalah sudut antara kedua vektor.
Ilustrasi: Bayangkan dua gaya bekerja pada poros yang sama. Cross product menghitung gaya total yang akan membuat objek berputar di sekitar poros tersebut, sehingga vektor hasilnya tegak lurus terhadap bidang kedua gaya tersebut.
Contoh Cross Product:
Jika kita memiliki dua vektor A dan B yang tidak searah, cross product mereka akan menghasilkan vektor baru yang tegak lurus terhadap bidang yang dibentuk oleh A dan B.
Jika besar vektor A adalah 5 dan besar vektor B adalah 4, dengan sudut 90 derajat, maka cross product mereka adalah:
![]()
Vektor hasilnya tegak lurus terhadap bidang yang dibentuk oleh A dan B.
Aplikasi dan Penggunaan Vektor dalam Kehidupan Sehari-hari
Vektor memiliki peran penting dalam berbagai aspek kehidupan sehari-hari dan sains. Berikut adalah beberapa aplikasi penting dari sifat-sifat vektor:
1. Vektor dalam Fisika dan Teknik
Dalam fisika, vektor digunakan untuk merepresentasikan besaran seperti gaya, kecepatan, dan percepatan. Sifat-sifat vektor membantu kita menghitung resultan gaya, menentukan arah gerak, dan menghitung energi yang dihasilkan oleh suatu sistem.
Misalnya, dalam perhitungan torsi (momen gaya), kita menggunakan cross product untuk menghitung besar dan arah torsi yang dihasilkan oleh gaya yang bekerja pada jarak tertentu dari poros putaran.
2. Navigasi dan GPS
Navigasi dan sistem GPS menggunakan vektor untuk menentukan posisi dan arah. Lokasi suatu titik pada peta dapat dinyatakan dalam bentuk koordinat vektor, dan arah pergerakan dapat dihitung dengan menggunakan vektor kecepatan.
Ilustrasi: Bayangkan peta dengan titik-titik yang menunjukkan lokasi Anda. Setiap titik dapat dinyatakan sebagai vektor dari titik awal, dan pergerakan dari satu titik ke titik lain menggunakan operasi penjumlahan vektor untuk mendapatkan arah dan jarak.
3. Keseimbangan Benda dan Konstruksi
Dalam konstruksi dan rekayasa struktural, sifat-sifat vektor digunakan untuk menghitung keseimbangan gaya pada struktur. Setiap gaya yang bekerja pada suatu benda dihitung dan digabungkan, sehingga insinyur dapat memastikan bahwa struktur tersebut stabil dan seimbang.
Misalnya, dalam perhitungan jembatan atau gedung, insinyur menggunakan vektor untuk menghitung semua gaya yang bekerja pada struktur tersebut, termasuk gaya tarik dan tekan, untuk memastikan bahwa bangunan dapat berdiri kokoh tanpa miring atau runtuh.
4. Olahraga dan Biomekanika
Dalam bidang olahraga dan biomekanika, vektor digunakan untuk menganalisis gerakan tubuh. Gaya yang diberikan oleh otot, arah gerak tubuh, serta kecepatan gerak dapat dianalisis menggunakan vektor. Ini membantu atlet dan pelatih memahami efisiensi gerakan dan memperbaiki teknik mereka.
Ilustrasi: Bayangkan seorang pelari yang berlari ke depan sambil menghasilkan gaya dorong dengan kaki mereka. Gerakannya dapat dihitung dalam bentuk vektor, yang menunjukkan arah dan besar kecepatan, sehingga pelatih dapat mengukur seberapa efisien gerakan lari tersebut.
Kesimpulan
Sifat-sifat vektor adalah dasar dalam memahami bagaimana berbagai besaran yang memiliki arah beroperasi dalam ruang. Dari penjumlahan dan pengurangan vektor, hingga operasi dot product dan cross product, semua sifat ini membantu kita dalam memahami dan menyelesaikan berbagai masalah yang melibatkan arah dan besar. Aplikasi vektor tidak hanya terbatas pada matematika atau fisika, tetapi juga meluas ke berbagai bidang seperti navigasi, teknik, olahraga, dan keseimbangan struktur. Dengan memahami vektor dan sifat-sifatnya, kita bisa mengatasi banyak tantangan yang melibatkan gerakan, gaya, dan perubahan arah dalam kehidupan sehari-hari.
