Vektor – Apa itu, Pengertian, Ciri-ciri, Jenis dan Contohnya

Vektor adalah salah satu konsep fundamental dalam matematika dan fisika yang memiliki banyak aplikasi dalam berbagai bidang, termasuk ilmu komputer, teknik, dan ekonomi. Vektor tidak hanya digunakan untuk menggambarkan besaran fisik seperti gaya dan kecepatan, tetapi juga untuk merepresentasikan data dalam analisis statistik dan machine learning. Dalam artikel ini, kita akan membahas secara mendalam tentang apa itu vektor, jenis-jenis vektor, operasi yang dapat dilakukan pada vektor, serta aplikasinya dalam berbagai disiplin ilmu.

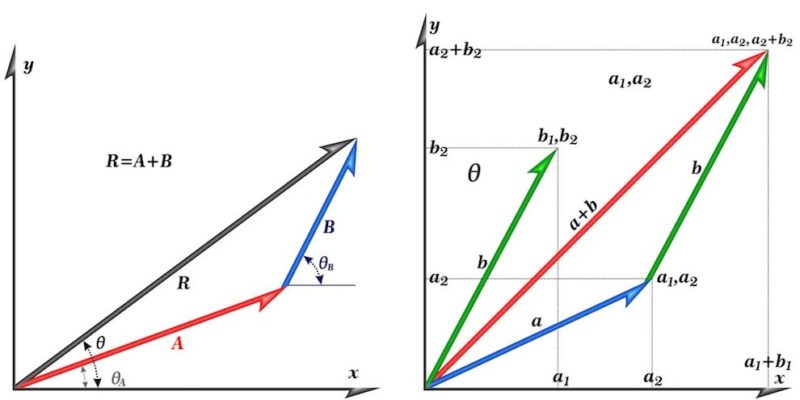
Dalam matematika, vektor adalah sebuah objek yang memiliki magnitude (besar) dan arah. Vektor digunakan untuk menggambarkan besaran fisik seperti kecepatan, percepatan, gaya, dan banyak lagi. Vektor merupakan konsep penting dalam berbagai bidang ilmu, termasuk matematika, fisika, dan teknik.

Definisi Vektor

Secara sederhana, vektor adalah suatu entitas matematika yang memiliki dua komponen utama: arah dan magnitudo (besar). Vektor sering kali digambarkan sebagai panah yang menunjukkan arah dan panjang panah tersebut menunjukkan magnitudo. Dalam notasi matematis, vektor biasanya dilambangkan dengan huruf tebal atau huruf dengan tanda panah di atasnya, seperti v atau $\vec{v}$ .

Vektor dapat dinyatakan dalam bentuk koordinat. Misalnya, vektor dalam ruang dua dimensi dapat dituliskan sebagai $\vec{v} = (x, y)$ , di mana $x$ dan $y$ adalah komponen vektor pada sumbu x dan y. Dalam ruang tiga dimensi, vektor dapat dituliskan sebagai $\vec{v} = (x, y, z)$ .

Jenis-jenis Vektor

Vektor dapat diklasifikasikan ke dalam beberapa jenis berdasarkan berbagai kriteria. Berikut adalah beberapa jenis vektor yang umum digunakan:

1. Vektor Positif dan Negatif:
– Vektor Positif: Vektor yang memiliki arah yang sama dengan arah referensi. Contoh: Vektor yang menunjukkan gerakan ke kanan pada sumbu x.
– Vektor Negatif: Vektor yang memiliki arah berlawanan dengan arah referensi. Contoh: Vektor yang menunjukkan gerakan ke kiri pada sumbu x.

2. Vektor Nol: Vektor yang tidak memiliki magnitudo dan arah. Dalam notasi, vektor nol biasanya dilambangkan dengan $\vec{0}$ dan dapat dinyatakan sebagai $\vec{0} = (0, 0)$ dalam dua dimensi atau $\vec{0} = (0, 0, 0)$ dalam tiga dimensi.

3. Vektor Unit: Vektor yang memiliki magnitudo satu. Vektor unit digunakan untuk menunjukkan arah tanpa memperhatikan besaran. Contoh: Vektor unit dalam arah sumbu x dapat dinyatakan sebagai $\hat{i} = (1, 0)$ dan dalam arah sumbu y sebagai $\hat{j} = (0, 1)$ .

4. Vektor Kolinier: Dua atau lebih vektor dikatakan kolinier jika mereka terletak pada garis yang sama atau sejajar. Vektor kolinier dapat memiliki arah yang sama atau berlawanan.

5. Vektor Ortogonal: Dua vektor dikatakan ortogonal jika sudut di antara keduanya adalah 90 derajat. Dalam hal ini, hasil kali dot (dot product) dari kedua vektor tersebut adalah nol.

Operasi pada Vektor

Ada beberapa operasi dasar yang dapat dilakukan pada vektor. Berikut adalah beberapa operasi yang paling umum:

1. Penjumlahan Vektor: Penjumlahan vektor dilakukan dengan menjumlahkan komponen-komponen vektor. Misalkan $\vec{a} = (a_1, a_2)$ dan $\vec{b} = (b_1, b_2)$ , maka penjumlahan vektor dapat dinyatakan sebagai:

$\vec{c} = \vec{a} + \vec{b} = (a_1 + b_1, a_2 + b_2)$

Contoh: Jika $\vec{a} = (2, 3)$ dan $\vec{b} = (4, 1)$ , maka $\vec{c} = (2 + 4, 3 + 1) = (6, 4)$ .

2. Pengurangan Vektor: Pengurangan vektor dilakukan dengan mengurangkan komponen-komponen vektor. Misalkan $\vec{a} = (a_1, a_2)$ dan $\vec{b} = (b_1, b_2)$ , maka pengurangan vektor dapat dinyatakan sebagai:

$\vec{c} = \vec{a} - \vec{b} = (a_1 - b_1, a_2 - b_2)$

Contoh: Jika $\vec{a} = (5, 7)$ dan $\vec{b} = (3, 2)$ , maka $\vec{c} = (5 - 3, 7 - 2) = (2, 5)$ .

3. Perkalian Vektor dengan Skalar: Vektor dapat dikalikan dengan bilangan skalar, yang akan mengubah magnitudo vektor tanpa mengubah arah. Jika $\vec{a} = (a_1, a_2)$ dan $k$ adalah skalar, maka:

$\vec{b} = k \cdot \vec{a} = (k \cdot a_1, k \cdot a_2)$

Contoh: Jika $\vec{a} = (3, 4)$ dan $k = 2$ , maka $\vec{b} = 2 \cdot (3, 4) = (6, 8)$ .

4. Hasil Kali Dot (Dot Product): Hasil kali dot dari dua vektor $\vec{a} = (a_1, a_2)$ dan $\vec{b} = (b_1, b_2)$ didefinisikan sebagai:

$\vec{a} \cdot \vec{b} = a_1 \cdot b_1 + a_2 \cdot b_2$

Hasil kali dot memberikan informasi tentang seberapa besar dua vektor saling berhubungan. Jika hasil kali dot adalah nol, maka kedua vektor tersebut ortogonal.

5. Hasil Kali Silang (Cross Product): Hasil kali silang hanya didefinisikan untuk vektor dalam ruang tiga dimensi. Jika $\vec{a} = (a_1, a_2, a_3)$ dan $\vec{b} = (b_1, b_2, b_3)$ , maka hasil kali silang didefinisikan sebagai:

$\vec{a} \times \vec{b} = (a_2b_3 - a_3b_2, a_3b_1 - a_1b_3, a_1b_2 - a_2b_1)$

Hasil kali silang menghasilkan vektor yang ortogonal terhadap kedua vektor yang dikalikan.

Aplikasi Vektor dalam Berbagai Bidang

Vektor memiliki banyak aplikasi dalam berbagai disiplin ilmu. Berikut adalah beberapa contoh aplikasi vektor:

1. Fisika: Dalam fisika, vektor digunakan untuk menggambarkan besaran fisik seperti gaya, kecepatan, percepatan, dan momentum. Misalnya, gaya yang bekerja pada suatu objek dapat dinyatakan sebagai vektor yang menunjukkan arah dan besarnya gaya tersebut.

2. Grafika Komputer: Dalam grafika komputer, vektor digunakan untuk merepresentasikan gambar dan objek dalam ruang dua dan tiga dimensi. Vektor memungkinkan pemodelan objek yang lebih kompleks dan realistis.

3. Statistika dan Analisis Data: Dalam analisis data, vektor digunakan untuk merepresentasikan data multivariat. Setiap observasi dapat dianggap sebagai vektor dalam ruang berdimensi tinggi, di mana setiap dimensi mewakili variabel yang berbeda.

4. Machine Learning: Dalam machine learning, vektor digunakan untuk merepresentasikan fitur dari data. Algoritma pembelajaran mesin sering kali bekerja dengan vektor untuk melakukan klasifikasi, regresi, dan pengelompokan.

5. Robotika: Dalam robotika, vektor digunakan untuk menggambarkan posisi dan orientasi robot dalam ruang. Vektor juga digunakan dalam perhitungan lintasan dan kontrol gerakan robot.

Kesimpulan

Vektor adalah konsep yang sangat penting dalam matematika dan ilmu pengetahuan, dengan banyak aplikasi dalam berbagai bidang. Memahami definisi, jenis, operasi, dan aplikasi vektor dapat membantu kita dalam menganalisis dan memecahkan masalah yang kompleks. Dengan pemahaman yang baik tentang vektor, kita dapat menerapkan konsep ini dalam fisika, grafika komputer, analisis data, machine learning, dan banyak lagi. Oleh karena itu, penting bagi setiap individu yang terlibat dalam bidang-bidang tersebut untuk memiliki pemahaman yang kuat tentang vektor dan aplikasinya. Dengan demikian, kita dapat lebih efektif dalam menggunakan vektor untuk menggambarkan dan menganalisis fenomena di dunia nyata.

Pengayaan.com

Related Posts

Sifat-sifat Vektor dalam Matematika dan Fisika