Advantages and Disadvantages of the Bisection Method

The bisection method is a numerical technique used for finding the roots of a continuous function. This iterative method relies on the Intermediate Value Theorem, which states that if a function changes sign over an interval, there exists at least one root within that interval. The bisection method involves repeatedly dividing the interval in half and determining in which subinterval the root lies. While this method is widely used for its simplicity and reliability, it also has its limitations. This article explores the advantages and disadvantages of the bisection method, providing insights into its practical applications.

Understanding the Bisection Method

What is the Bisection Method?

The Bisection Method is a root-finding algorithm that repeatedly bisects an interval and selects a subinterval in which a root must lie. It is a simple yet effective method for finding roots of continuous functions, particularly when the function is continuous and the root is bracketed between two points.

Illustrative Explanation

To visualize the Bisection Method, consider a continuous function plotted on a Cartesian plane. If we want to find the root of the equation , we start with two initial points and such that:

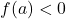• (the function value at is negative)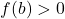
• (the function value at 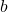is positive)

This indicates that there is at least one root in the interval . The Bisection Method will iteratively narrow down this interval until it converges to the root.

f(x)
|
|          *
|         * *
|        *   *
|       *     *
|      *       *
|     *         *
|    *           *
|   *             *
|  *               *
| *                 *
|*                   *
+---------------------+---- x
a b

In this diagram, the curve represents the function , and the points and are the initial guesses. The root lies somewhere between these two points.

Steps of the Bisection Method

The Bisection Method follows a systematic approach to find the root of a function. Here are the steps involved:

Step 1: Choose Initial Points

Select two initial points and such that and . This ensures that there is at least one root in the interval .

Step 2: Calculate the Midpoint

Calculate the midpoint of the interval :

   

Step 3: Evaluate the Function at the Midpoint

Evaluate the function at the midpoint:

   

Step 4: Determine the Subinterval

Now, determine which subinterval contains the root:

• If 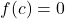, then is the root, and the process stops.
• If 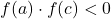, then the root lies in the interval . Set .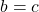
• If 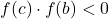, then the root lies in the interval . Set .

Step 5: Repeat the Process

Repeat Steps 2 to 4 until the desired level of accuracy is achieved, or until the interval is sufficiently small.

Step 6: Convergence

The process converges to the root as the interval narrows down. The final approximation of the root can be taken as the midpoint of the last interval.

Example of the Bisection Method

To illustrate the Bisection Method, let’s find the root of the function in the interval .

Step-by-Step Calculation

1. Choose Initial Points:
– Let and .
– Evaluate and :
– (negative)
– (positive)

2. Calculate the Midpoint:

   

3. Evaluate the Function at the Midpoint:

   

4. Determine the Subinterval:
– Since and , the root lies in the interval . Set .

5. Repeat the Process:
– Calculate the new midpoint:

   

– Evaluate:

   

– Since and , the root lies in the interval . Set .

6. Continue Iterating:
– Calculate the next midpoint:

   

– Evaluate:

   

– The root lies in . Set .

7. Further Iterations:
– Continue this process until the interval is sufficiently small. After several iterations, you will converge to the root .

Convergence and Error Analysis

Convergence of the Bisection Method

The Bisection Method is guaranteed to converge to a root as long as the initial interval contains a root and the function is continuous. The convergence is linear, meaning that the error decreases by half with each iteration.

Error Estimation

The error in the Bisection Method can be estimated as:

   

This formula indicates that the error is half the width of the current interval. As the iterations progress, the error decreases, leading to a more accurate approximation of the root.

Advantages and Disadvantages of the Bisection Method

Advantages of the Bisection Method

1. Simplicity and Ease of Implementation

One of the most significant advantages of the bisection method is its simplicity. The algorithm is straightforward, making it easy to understand and implement, even for those with limited mathematical backgrounds. The basic steps involve evaluating the function at the endpoints of the interval and repeatedly narrowing down the search space until the root is found within a desired tolerance. This simplicity is particularly beneficial in educational settings, where students can quickly grasp the concept of root-finding without delving into more complex methods.

2. Guaranteed Convergence

The bisection method provides a guaranteed convergence to a root, as long as the initial interval is chosen correctly and the function is continuous. Since the method relies on the Intermediate Value Theorem, it ensures that the root will be located within the interval where the function changes sign. Unlike some other numerical methods that may fail to converge or can be sensitive to initial guesses, the bisection method offers a reliable approach to root-finding.

3. Robustness

The bisection method is particularly robust and can handle a wide variety of functions, including those that are nonlinear or have multiple roots. It does not require the function to be differentiable, making it applicable to a broader range of problems. This robustness makes the method a valuable tool in situations where other methods might struggle or fail, such as when dealing with discontinuous functions or functions with complicated behavior.

4. Control Over Accuracy

The bisection method allows users to control the accuracy of the root approximation. By specifying a tolerance level for the desired accuracy, users can dictate how close the final approximation should be to the actual root. This flexibility is useful in practical applications where different levels of precision are required depending on the context of the problem.

Disadvantages of the Bisection Method

1. Slow Convergence Rate

One of the primary disadvantages of the bisection method is its relatively slow convergence rate compared to other root-finding algorithms, such as Newton’s method or the secant method. The bisection method converges linearly, meaning that the number of correct digits approximately doubles with each iteration. As a result, it can require a significantly larger number of iterations to achieve a high level of precision, making it less efficient for problems that demand rapid solutions.

2. Requires a Bracketing Interval

The bisection method necessitates the identification of a bracketing interval that contains the root. This requirement means that the user must have prior knowledge of the function’s behavior in the specified interval to ensure that it contains a root. In cases where the function is complex or the root is not easily identifiable, determining an appropriate interval can be challenging and may require additional analysis.

3. Limited to One Root at a Time

The bisection method is designed to find a single root within a given interval, which can be a limitation in scenarios where multiple roots exist. If the function has several roots, the method will only converge to the root within the specified interval, potentially overlooking other roots that may be of interest. This characteristic necessitates the use of additional techniques to locate all roots within a function.

4. Function Evaluations Can Be Computationally Expensive

While the bisection method is simple, it requires multiple evaluations of the function at each iteration. For functions that are computationally expensive to evaluate, this can lead to increased processing time, especially when high precision is required. In such cases, other methods that require fewer function evaluations or utilize derivative information may be more efficient.

Applications of the Bisection Method

The Bisection Method has numerous applications across various fields:

1. Mathematics

In mathematics, the Bisection Method is used to find roots of equations, particularly in calculus and numerical analysis.

2. Engineering

Engineers use the Bisection Method in design and analysis, especially when dealing with nonlinear equations that arise in structural analysis, fluid dynamics, and thermodynamics.

3. Computer Science

In computer science, the Bisection Method is employed in algorithms for root-finding problems, optimization, and numerical simulations.

4. Physics

Physicists use the Bisection Method to solve equations related to motion, energy, and other physical phenomena where analytical solutions are difficult to obtain.

5. Finance

In finance, the Bisection Method can be used to find interest rates, investment returns, and other financial metrics that require solving equations.

Conclusion

In conclusion, the bisection method is a valuable numerical technique for finding roots of continuous functions, offering several advantages, including simplicity, guaranteed convergence, robustness, and control over accuracy. However, it also has notable disadvantages, such as slow convergence, the need for a bracketing interval, limitations in finding multiple roots, and potential computational inefficiencies.

When choosing a root-finding method, it is essential to consider the specific requirements of the problem at hand. While the bisection method may not always be the fastest or most efficient option, its reliability and ease of implementation make it a useful tool in many mathematical and engineering applications. Understanding both its strengths and limitations can help practitioners make informed decisions when tackling root-finding challenges.