Understanding Ampere’s Law: A Comprehensive Overview

Ampere’s Law is a fundamental principle in electromagnetism that relates the magnetic field around a closed loop to the electric current passing through that loop. Named after the French physicist André-Marie Ampère, this law is crucial for understanding how electric currents generate magnetic fields and is foundational in the study of electromagnetism, electrical engineering, and physics. This article will provide a detailed exploration of Ampere’s Law, including its mathematical formulation, applications, illustrative explanations, and its significance in various fields.

1. Definition of Ampere’s Law

Ampere’s Law states that the line integral of the magnetic field ( $\mathbf{B}$ ) around a closed loop is equal to the permeability of free space ( $\mu_0$ ) multiplied by the total electric current ( $I$ ) passing through the loop. Mathematically, it can be expressed as:

$\oint \mathbf{B} \cdot d\mathbf{l} = \mu_0 I_{enc}$

Where:

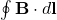$\oint \mathbf{B} \cdot d\mathbf{l}$ is the line integral of the magnetic field around a closed path,
$\mu_0$ is the permeability of free space (approximately $4\pi \times 10^{-7} \, \text{T m/A}$ ),
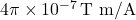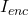$I_{enc}$ is the total current enclosed by the path.

Illustrative Explanation: Imagine a circular path drawn around a wire carrying an electric current. According to Ampere’s Law, if you were to measure the magnetic field along this circular path, the total magnetic field multiplied by the length of the path would equal the current flowing through the wire multiplied by a constant factor ( $\mu_0$ ). This relationship shows how electric currents create magnetic fields.

2. Understanding the Components of Ampere’s Law

A. Magnetic Field (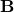 $\mathbf{B}$ )

The magnetic field is a vector field that describes the magnetic influence of electric charges in relative motion and magnetized materials. It is measured in teslas (T) and can be visualized as lines of force emanating from magnetic poles.

Illustrative Explanation: Picture a bar magnet. The magnetic field lines emerge from the north pole and enter the south pole, creating a pattern that can be visualized with iron filings sprinkled around the magnet. The density of these lines indicates the strength of the magnetic field.

B. Line Integral (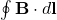 $\oint \mathbf{B} \cdot d\mathbf{l}$ )

The line integral of the magnetic field around a closed loop quantifies the total magnetic field along that path. It involves integrating the magnetic field vector along the path length, taking into account the direction of the field relative to the path.

Illustrative Explanation: If you were to walk along a circular path around a current-carrying wire, the line integral would sum up the contributions of the magnetic field at each point along your path. If the magnetic field is uniform and circular, this integral simplifies to $B \times L$ , where $L$ is the circumference of the path.

C. Permeability of Free Space ( $\mu_0$ )

The permeability of free space is a constant that characterizes the ability of a vacuum to support the formation of magnetic fields. It is a fundamental physical constant that plays a crucial role in electromagnetism.

Illustrative Explanation: Think of $\mu_0$ as a measure of how easily magnetic field lines can pass through space. In a vacuum, this value is constant, but in materials, the permeability can vary, affecting how magnetic fields behave.

D. Enclosed Current (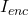 $I_{enc}$ )

The enclosed current is the total current that passes through the surface bounded by the closed loop. This current generates the magnetic field that is being measured.

Illustrative Explanation: If you have multiple wires carrying currents, the total current that contributes to the magnetic field around a specific loop is the sum of the currents that pass through that loop. For example, if two wires carry currents of 3 A and 5 A, the total enclosed current would be 8 A if both currents pass through the loop.

3. Applications of Ampere’s Law

Ampere’s Law has numerous applications in both theoretical and practical contexts, including:

A. Magnetic Field Calculation

Ampere’s Law is often used to calculate the magnetic field generated by symmetrical current distributions, such as long straight wires, solenoids, and toroids.

Illustrative Explanation: For a long straight wire carrying a current $I$ , the magnetic field at a distance $r$ from the wire can be derived using Ampere’s Law. The result is given by:

$B = \frac{\mu_0 I}{2\pi r}$

This equation shows that the magnetic field decreases with distance from the wire, illustrating how the strength of the magnetic field diminishes as you move away from the source of the current.

B. Electromagnetic Devices

Ampere’s Law is fundamental in the design and operation of various electromagnetic devices, such as electric motors, transformers, and inductors. Understanding how currents generate magnetic fields allows engineers to create efficient devices.

Illustrative Explanation: In an electric motor, current flows through coils of wire, generating a magnetic field that interacts with permanent magnets. This interaction produces torque, causing the motor to spin. Ampere’s Law helps engineers calculate the required current and coil design to achieve the desired performance.

C. Magnetic Field Mapping

Ampere’s Law is used in magnetic field mapping, which is essential for understanding the behavior of magnetic fields in different environments, such as in the vicinity of electrical equipment or in geological surveys.

Illustrative Explanation: When mapping the magnetic field around a power line, engineers can use Ampere’s Law to predict how the magnetic field will behave at various distances from the line. This information is crucial for ensuring safety and compliance with regulations.

4. Limitations of Ampere’s Law

While Ampere’s Law is a powerful tool, it has limitations, particularly in cases involving non-static or time-varying fields. In such situations, the law must be modified to account for additional factors.

A. Time-Varying Fields

Ampere’s Law, in its original form, does not account for situations where the electric field changes with time. In these cases, Maxwell’s addition to Ampere’s Law introduces the concept of displacement current, which accounts for changing electric fields.

Illustrative Explanation: Consider a capacitor being charged. As the electric field between the plates changes, the displacement current must be included in the calculations to accurately describe the magnetic field around the capacitor. The modified form of Ampere’s Law is:

$\oint \mathbf{B} \cdot d\mathbf{l} = \mu_0 \left( I_{enc} + \epsilon_0 \frac{d\Phi_E}{dt} \right)$

Where $\epsilon_0$ is the permittivity of free space and $\frac{d\Phi_E}{dt}$ is the rate of change of the electric flux.

B. Complex Geometries

Ampere’s Law is most effective for symmetrical situations. In cases with complex geometries or non-uniform current distributions, applying the law can be challenging, and numerical methods or computational techniques may be required.

Illustrative Explanation: If you have a complex arrangement of wires with varying currents, calculating the magnetic field using Ampere’s Law directly may not yield straightforward results. In such cases, numerical simulations or advanced techniques like finite element analysis may be necessary to accurately model the magnetic field.

5. Conclusion

In summary, Ampere’s Law is a fundamental principle in electromagnetism that describes the relationship between electric currents and the magnetic fields they generate. By understanding the components of Ampere’s Law, including magnetic fields, line integrals, permeability, and enclosed currents, we can apply this law to various practical applications, from calculating magnetic fields around wires to designing electromagnetic devices. While Ampere’s Law has limitations, particularly in time-varying fields and complex geometries, it remains a cornerstone of electromagnetic theory and a vital tool for engineers and physicists alike. By grasping the principles of Ampere’s Law, we can better appreciate the intricate connections between electricity and magnetism that govern much of the physical world.

Blog.Pengayaan.Com

Understanding Ampere’s Law: A Comprehensive Overview

1. Definition of Ampere’s Law