Area of a Hemisphere: A Comprehensive Guide

Math
Comments

The concept of a hemisphere is fundamental in geometry, particularly in the study of three-dimensional shapes. A hemisphere is essentially half of a sphere, and understanding its area is crucial for various applications in mathematics, physics, engineering, and real-world problem-solving. This article will provide a detailed exploration of the area of a hemisphere, including its definition, formulas, derivation, properties, and illustrative explanations to enhance understanding.

1. Definition of a Hemisphere

A hemisphere is defined as half of a sphere. It is created when a sphere is divided into two equal halves by a plane that passes through its center. The flat circular face of the hemisphere is called the base, while the curved surface is the lateral surface.

Illustrative Explanation:

Imagine a basketball. If you were to slice it perfectly in half through its center, you would have two hemispheres. Each hemisphere retains the curved surface of the sphere and has a flat circular base.

2. Formulas for the Area of a Hemisphere

The area of a hemisphere can be divided into two components:
1. The curved surface area (CSA).
2. The base area (the area of the circular face).

A. Curved Surface Area (CSA)

The formula for the curved surface area of a hemisphere is given by:

    \[ \text{Curved Surface Area (CSA)} = 2\pi r^2 \]

Where:

  • r is the radius of the hemisphere.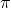
  • \pi (pi) is a mathematical constant approximately equal to 3.14159.

B. Base Area

The formula for the area of the base (which is a circle) is given by:

    \[ \text{Base Area} = \pi r^2 \]

C. Total Surface Area

The total surface area (TSA) of a hemisphere combines both the curved surface area and the base area:

    \[ \text{Total Surface Area (TSA)} = \text{Curved Surface Area} + \text{Base Area} \]

Substituting the formulas, we get:

    \[ \text{Total Surface Area (TSA)} = 2\pi r^2 + \pi r^2 = 3\pi r^2 \]

Illustrative Explanation:

If you have a hemisphere with a radius of 3 units:

  • The curved surface area would be 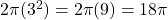2\pi(3^2) = 2\pi(9) = 18\pi square units.
  • The base area would be 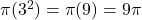\pi(3^2) = \pi(9) = 9\pi square units.
  • Therefore, the total surface area would be 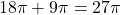18\pi + 9\pi = 27\pi square units.

3. Derivation of the Formulas

A. Curved Surface Area Derivation

To derive the formula for the curved surface area of a hemisphere, consider the following:

1. Understanding the Sphere: The surface area of a complete sphere is given by the formula:

    \[ \text{Surface Area of Sphere} = 4\pi r^2 \]

2. Halving the Sphere: Since a hemisphere is half of a sphere, the curved surface area of the hemisphere is half of the total surface area of the sphere:

    \[ \text{Curved Surface Area} = \frac{1}{2} \times 4\pi r^2 = 2\pi r^2 \]

B. Base Area Derivation

The base of the hemisphere is a circle with radius r. The area of a circle is given by:

    \[ \text{Area of Circle} = \pi r^2 \]

Thus, the base area of the hemisphere is simply \pi r^2.

C. Total Surface Area Derivation

As derived earlier, the total surface area combines both the curved surface area and the base area:

    \[ \text{Total Surface Area} = 2\pi r^2 + \pi r^2 = 3\pi r^2 \]

4. Properties of a Hemisphere

Understanding the properties of a hemisphere can provide deeper insights into its geometric characteristics:

A. Symmetry:

A hemisphere is symmetric about its vertical axis. This means that if you were to slice it down the middle, both halves would be mirror images of each other.

B. Volume:

The volume of a hemisphere can also be calculated, which is given by the formula:

    \[ \text{Volume} = \frac{2}{3}\pi r^3 \]

This formula is derived from the volume of a sphere, which is \frac{4}{3}\pi r^3, and halving it for the hemisphere.

C. Curved Surface:

The curved surface of a hemisphere is a continuous, smooth surface that can be described mathematically using parametric equations or spherical coordinates.

5. Applications of the Area of a Hemisphere

The area of a hemisphere has various applications across different fields:

A. Engineering:

In engineering, hemispherical shapes are often used in the design of tanks, domes, and other structures. Understanding the surface area is crucial for material calculations and structural integrity.

B. Architecture:

Architects use hemispherical designs in buildings and structures, such as domes and roofs. The area calculations help in determining the amount of materials needed for construction.

C. Physics:

In physics, hemispherical shapes are used in optics and acoustics. For example, hemispherical lenses and reflectors are designed based on their surface area properties.

D. Geography:

In geography, hemispherical models are used to represent the Earth and its features. Understanding the area helps in mapping and spatial analysis.

6. Conclusion

The area of a hemisphere is a fundamental concept in geometry that encompasses both the curved surface area and the base area. By understanding the formulas, derivations, and properties of a hemisphere, individuals can apply this knowledge in various fields, from engineering to architecture.

Key Takeaways:

  • A hemisphere is half of a sphere, characterized by a curved surface and a flat circular base.
  • The curved surface area is given by 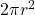2\pi r^2, while the base area is \pi r^2.
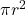  • The total surface area of a hemisphere is 3\pi r^2.
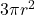  • The volume of a hemisphere is \frac{2}{3}\pi r^3.
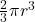  • Hemispheres have practical applications in engineering, architecture, physics, and geography.

By mastering the concept of the area of a hemisphere, individuals can enhance their geometric understanding and apply these principles effectively in real-world scenarios, leading to a deeper appreciation of the beauty and utility of mathematics.

Updated: February 14, 2025 — 16:40

Leave a Reply

Your email address will not be published. Required fields are marked *