The area of a quadrilateral is a fundamental concept in geometry that pertains to the measurement of the space enclosed within a four-sided polygon. Quadrilaterals are diverse shapes that include squares, rectangles, parallelograms, trapezoids, and rhombuses, each with unique properties and formulas for calculating their area. This article aims to provide an exhaustive exploration of the area of quadrilaterals, including definitions, formulas, methods of calculation, and illustrative explanations to enhance understanding.
1. Definition of a Quadrilateral
A quadrilateral is a polygon with four edges (sides) and four vertices (corners). The sum of the interior angles of a quadrilateral is always 
. Quadrilaterals can be classified into several categories based on their properties:
- Convex Quadrilaterals: All interior angles are less than
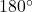. - Concave Quadrilaterals: At least one interior angle is greater than .
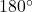- Regular Quadrilaterals: All sides and angles are equal (e.g., a square).
Illustrative Explanation
To visualize a quadrilateral, imagine a simple shape like a rectangle. It has four sides, four corners, and the angles at each corner are 
. Now, consider a more complex shape like a kite, which also has four sides but with two pairs of adjacent sides that are equal in length. Both shapes are quadrilaterals, but they exhibit different properties.
2. Area Formulas for Different Types of Quadrilaterals
The area of a quadrilateral can be calculated using various formulas depending on its specific type. Below are the most common types of quadrilaterals and their respective area formulas:
2.1. Rectangle
A rectangle is a quadrilateral with opposite sides that are equal in length and all angles equal to .
Area Formula:
![\[ \text{Area} = \text{length} \times \text{width} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-7a9a02f0392fb496d46e62e9728edf0d_l3.png "Rendered by QuickLaTeX.com")
Example Calculation
If a rectangle has a length of 
and a width of 
, the area can be calculated as follows:
![\[ \text{Area} = 5 \, \text{cm} \times 3 \, \text{cm} = 15 \, \text{cm}^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-135dfe7d33f2667161fb16bff31d4e01_l3.png "Rendered by QuickLaTeX.com")
2.2. Square
A square is a special type of rectangle where all four sides are equal in length.
Area Formula:
![\[ \text{Area} = \text{side}^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-c4c7f8ae427a46b234a62e3f2feb39d2_l3.png "Rendered by QuickLaTeX.com")
Example Calculation
For a square with a side length of 
:
![\[ \text{Area} = 4 \, \text{cm} \times 4 \, \text{cm} = 16 \, \text{cm}^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-9d54891b90bfa9a059b08dc94fe99ae7_l3.png "Rendered by QuickLaTeX.com")
2.3. Parallelogram
A parallelogram is a quadrilateral with opposite sides that are equal and parallel.
Area Formula:
![\[ \text{Area} = \text{base} \times \text{height} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-115a90fad84dbfa5caa22b0d8030b335_l3.png "Rendered by QuickLaTeX.com")
Example Calculation
If a parallelogram has a base of 
and a height of :
![\[ \text{Area} = 6 \, \text{cm} \times 4 \, \text{cm} = 24 \, \text{cm}^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-c5b508650ae33e5940cb2e8b1b1e73e3_l3.png "Rendered by QuickLaTeX.com")
2.4. Trapezoid (Trapezium)
A trapezoid is a quadrilateral with at least one pair of parallel sides.
Area Formula:
![\[ \text{Area} = \frac{1}{2} \times (\text{Base}_1 + \text{Base}_2) \times \text{height} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-30311745c1adcc0eeb18d7af79aac8f9_l3.png "Rendered by QuickLaTeX.com")
Example Calculation
For a trapezoid with bases of and , and a height of :
![\[ \text{Area} = \frac{1}{2} \times (5 \, \text{cm} + 3 \, \text{cm}) \times 4 \, \text{cm} = \frac{1}{2} \times 8 \, \text{cm} \times 4 \, \text{cm} = 16 \, \text{cm}^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-61498c1003b3e33687bf5be84f50d755_l3.png "Rendered by QuickLaTeX.com")
2.5. Rhombus
A rhombus is a quadrilateral with all sides equal in length, and opposite angles are equal.
Area Formula:
![\[ \text{Area} = \frac{1}{2} \times d_1 \times d_2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-fa0f1aed8b6892ffce9d63ca3a68fa70_l3.png "Rendered by QuickLaTeX.com")
where 
and 
are the lengths of the diagonals.
Example Calculation
If a rhombus has diagonals of and 
:
![\[ \text{Area} = \frac{1}{2} \times 6 \, \text{cm} \times 8 \, \text{cm} = \frac{1}{2} \times 48 \, \text{cm}^2 = 24 \, \text{cm}^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-febca158eeae3c76fd60eb85af220a25_l3.png "Rendered by QuickLaTeX.com")
3. Area of Irregular Quadrilaterals
For quadrilaterals that do not fit neatly into the categories above (irregular quadrilaterals), the area can be calculated using the following methods:
3.1. Divide and Conquer Method
One common approach is to divide the irregular quadrilateral into two triangles. The area of each triangle can be calculated using the formula:
![\[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-9cc90bc678ee66f478cad893b3da796d_l3.png "Rendered by QuickLaTeX.com")
Then, the total area of the quadrilateral is the sum of the areas of the two triangles.
Illustrative Explanation
Imagine an irregular quadrilateral that can be split into two triangles by drawing a diagonal. If one triangle has a base of and a height of , and the other triangle has a base of and a height of 
, the areas can be calculated as follows:
- Area of Triangle 1:
![\[ \text{Area}_1 = \frac{1}{2} \times 4 \, \text{cm} \times 3 \, \text{cm} = 6 \, \text{cm}^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-d7e3f982356025e4bc71a5199be7b2b6_l3.png "Rendered by QuickLaTeX.com")
- Area of Triangle 2:
![\[ \text{Area}_2 = \frac{1}{2} \times 5 \, \text{cm} \times 2 \, \text{cm} = 5 \, \text{cm}^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-76b70e39c827753f72d4d11420d026d0_l3.png "Rendered by QuickLaTeX.com")
- Total Area of Quadrilateral:
![\[ \text{Total Area} = 6 \, \text{cm}^2 + 5 \, \text{cm}^2 = 11 \, \text{cm}^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-96ae9c815820931e2bd5c29905a38568_l3.png "Rendered by QuickLaTeX.com")
3.2. Bretschneider’s Formula
For any quadrilateral, Bretschneider’s formula can be used to calculate the area when the lengths of all four sides and the measures of two opposite angles are known:
![\[ \text{Area} = \sqrt{(s-a)(s-b)(s-c)(s-d) - abcd \cdot \cos^2\left(\frac{B+D}{2}\right)} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-0ba91b924084ba37ac8f7d92cc7ea483_l3.png "Rendered by QuickLaTeX.com")
where 
is the semi-perimeter given by 
, and 
, 
, 
, and 
are the lengths of the sides.
Illustrative Explanation
Consider a quadrilateral with sides 
, 
, 
, and 
, and angles 
and 
. First, calculate the semi-perimeter:
![\[ s = \frac{5 + 6 + 7 + 8}{2} = 13 \, \text{cm} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-51247aab364671d3e8b8a185f8b1635c_l3.png "Rendered by QuickLaTeX.com")
Then, apply Bretschneider’s formula to find the area.
4. Conclusion
The area of a quadrilateral is a fundamental geometric concept that varies based on the type of quadrilateral being considered. From rectangles and squares to trapezoids and irregular shapes, each type has its own unique properties and formulas for calculating area. Understanding these concepts is essential for applications in mathematics, engineering, architecture, and various fields that require spatial reasoning.
In summary, whether you are calculating the area of a simple rectangle or an irregular quadrilateral, the principles outlined in this article provide a comprehensive framework for understanding and applying the concept of area in quadrilaterals. By mastering these formulas and methods, one can confidently tackle a wide range of geometric problems and applications.