Simple Harmonic Motion (SHM) is a fundamental concept in physics that describes the oscillatory motion of an object around an equilibrium position. This type of motion is characterized by a restoring force that is directly proportional to the displacement from the equilibrium position and acts in the opposite direction. SHM is prevalent in various physical systems, including pendulums, springs, and even in the behavior of certain waves. This article will provide an in-depth examination of simple harmonic motion, covering its definition, characteristics, mathematical formulation, examples, and applications, along with illustrative explanations to enhance understanding.
1. Definition of Simple Harmonic Motion
Simple Harmonic Motion is defined as a type of periodic motion in which an object moves back and forth around an equilibrium position in a regular, sinusoidal manner. The motion is called “simple” because it can be described by a single frequency and amplitude, and it follows a predictable pattern. The key feature of SHM is that the restoring force acting on the object is proportional to the displacement from the equilibrium position, which can be mathematically expressed as:
![]()
Where:
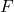 is the restoring force.
is the restoring force.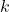 is the spring constant (a measure of the stiffness of the spring or the system).
is the spring constant (a measure of the stiffness of the spring or the system).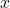 is the displacement from the equilibrium position.
is the displacement from the equilibrium position.
Illustrative Explanation: Imagine a child on a swing. When the swing is pulled back and released, it moves forward and backward around a central point (the equilibrium position). The force of gravity pulls the swing back toward the center, and the further the swing is pulled away from the center, the stronger the force pulling it back. This back-and-forth motion is a classic example of simple harmonic motion.
2. Characteristics of Simple Harmonic Motion
Simple Harmonic Motion has several defining characteristics that distinguish it from other types of motion:
- Periodic Motion: SHM is periodic, meaning it repeats itself at regular intervals. The time taken to complete one full cycle of motion is called the period (
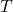 ).
). - Amplitude: The amplitude (
 ) of SHM is the maximum displacement from the equilibrium position. It represents the maximum extent of the oscillation.
) of SHM is the maximum displacement from the equilibrium position. It represents the maximum extent of the oscillation. - Frequency: The frequency (
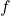 ) of SHM is the number of complete cycles that occur in one second. It is inversely related to the period:
) of SHM is the number of complete cycles that occur in one second. It is inversely related to the period:
![]()
- Phase: The phase of the motion describes the position of the oscillating object at a specific point in time. It is often expressed in radians and helps determine the state of the motion at any given moment.
- Restoring Force: The restoring force in SHM is always directed toward the equilibrium position and is proportional to the displacement. This characteristic ensures that the motion is oscillatory.
Illustrative Explanation: Consider a mass attached to a spring. When the mass is pulled down and released, it oscillates up and down. The maximum distance it moves from its resting position is the amplitude. The time it takes to return to the same position after one complete cycle is the period. The frequency tells us how many times the mass goes up and down in one second.
3. Mathematical Formulation of Simple Harmonic Motion
The motion of an object undergoing simple harmonic motion can be described mathematically using sine or cosine functions. The displacement ![]() of the object as a function of time can be expressed as:
of the object as a function of time can be expressed as:
![]()
Where:
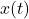 is the displacement at time
is the displacement at time 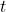 .
. is the amplitude of the motion.
is the amplitude of the motion.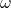 is the angular frequency, which is related to the frequency by the equation:
is the angular frequency, which is related to the frequency by the equation:
![]()
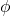 is the phase constant, which determines the starting position of the motion.
is the phase constant, which determines the starting position of the motion.
The velocity ![]() and acceleration
and acceleration ![]() of the object can also be derived from the displacement function:
of the object can also be derived from the displacement function:
- Velocity:
![]()
- Acceleration:
![]()
Where ![]() is the mass of the object.
is the mass of the object.
Illustrative Explanation: Visualize a pendulum swinging back and forth. At the highest point of its swing, the pendulum has maximum potential energy and zero kinetic energy. As it swings down, it accelerates, reaching maximum speed (and thus maximum kinetic energy) at the lowest point. The motion can be described using the equations above, where the displacement varies sinusoidally with time.
4. Examples of Simple Harmonic Motion
Simple Harmonic Motion can be observed in various physical systems. Here are a few illustrative examples:
- Mass-Spring System: A mass attached to a spring exhibits SHM when displaced from its equilibrium position. When the mass is pulled and released, it oscillates back and forth around the equilibrium position, with the restoring force provided by the spring.
- Pendulum: A simple pendulum, consisting of a mass (bob) attached to a string, also exhibits SHM for small angles of displacement. As the bob swings back and forth, it experiences a restoring force due to gravity, causing it to oscillate around its lowest point.
- Vibrating Tuning Fork: When a tuning fork is struck, its prongs vibrate back and forth, producing sound waves. The motion of the prongs can be modeled as SHM, with the restoring force provided by the elasticity of the material.
Illustrative Explanation: Imagine a mass on a spring. When you pull the mass down and let go, it bounces up and down. The distance it moves from the resting position is the amplitude, and the time it takes to complete one full bounce is the period. The motion is smooth and repetitive, characteristic of simple harmonic motion.
5. Applications of Simple Harmonic Motion
Simple Harmonic Motion has numerous practical applications across various fields:
- Engineering: SHM principles are used in the design of various mechanical systems, such as suspension systems in vehicles, where the oscillatory motion of springs helps absorb shocks and provide a smooth ride.
- Music: Musical instruments, such as guitars and pianos, rely on SHM to produce sound. The strings vibrate in simple harmonic motion, creating sound waves that correspond to musical notes.
- Seismology: The study of earthquakes involves analyzing the SHM of seismic waves. Understanding how these waves propagate helps scientists predict and mitigate the effects of earthquakes.
- Electronics: In electronic circuits, oscillators utilize SHM principles to generate alternating current (AC) signals. These signals are essential for various applications, including radio transmission and signal processing.
Illustrative Explanation: Consider a car’s suspension system. The springs in the suspension compress and expand as the car moves over bumps. This oscillatory motion helps keep the car stable and comfortable for passengers, demonstrating the practical application of simple harmonic motion in engineering.
Conclusion
Simple Harmonic Motion is a fundamental concept that plays a critical role in understanding various physical phenomena. By exploring the definitions, characteristics, mathematical formulations, examples, and applications of SHM, we gain a deeper appreciation for its significance in both natural and technological contexts. From the oscillations of a pendulum to the vibrations of a guitar string, simple harmonic motion is a powerful demonstration of the principles of oscillatory behavior. As we continue to study and apply these principles, we unlock new possibilities for innovation and understanding in the world around us.