The area of a segment of a circle is a fascinating concept in geometry that combines the properties of circles and triangles. A segment is defined as the region of a circle that is “cut off” from the rest of the circle by a chord. Understanding how to calculate the area of a segment is essential for various applications in mathematics, physics, engineering, and even art. This article will explore the definition of a segment of a circle, the formula for calculating its area, the derivation of the formula, and illustrative explanations to enhance comprehension.
Definition of a Segment of a Circle
What is a Segment of a Circle?
A segment of a circle is the area enclosed by a chord and the arc that connects the endpoints of the chord. It can be visualized as the “slice” of the circle that lies above or below the chord.
Illustrative Explanation
To visualize a segment of a circle, consider a circle with center 
and radius 
. Let 
be a chord of the circle. The area of the segment is the region bounded by the chord and the arc 
.
“` A / \ / \ / \ O------B “`
In this diagram, the shaded area represents the segment of the circle defined by chord and arc .
Formula for the Area of a Segment of a Circle
Mathematical Formula
The area 
of a segment of a circle can be calculated using the following formula:
![\[ A = \frac{r^2}{2} \left( \theta - \sin(\theta) \right) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-aa3d4d8740356a5e770f6285ab77da31_l3.png "Rendered by QuickLaTeX.com")
Where:
- = area of the segment
- = radius of the circle
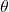= angle subtended by the chord at the center of the circle, measured in radians.
Illustrative Explanation of the Formula
The formula 
can be understood as follows:
- The term
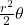represents the area of the sector formed by the angle 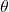at the center of the circle. - The term
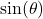accounts for the area of the triangle formed by the radius lines 
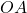and 
and 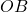the chord 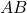. - By subtracting the area of the triangle from the area of the sector, we obtain the area of the segment.
Derivation of the Area Formula
To derive the area formula for a segment of a circle, we can break down the process into several steps.
1. Area of the Sector
The area of a sector of a circle is given by the formula:
![\[ A_{\text{sector}} = \frac{1}{2} r^2 \theta \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-48b5dd3aa3970954834dd3fea42426d5_l3.png "Rendered by QuickLaTeX.com")
This formula calculates the area of the sector formed by the angle at the center of the circle.
2. Area of the Triangle
Next, we need to calculate the area of the triangle 
formed by the two radii and and the chord . The area of triangle can be calculated using the formula:
![\[ A_{\text{triangle}} = \frac{1}{2} \times OA \times OB \times \sin(\theta) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-f4aedd6eacc4d84f7bd588e714444407_l3.png "Rendered by QuickLaTeX.com")
Since and are both equal to the radius , we can rewrite the area of the triangle as:
![\[ A_{\text{triangle}} = \frac{1}{2} r^2 \sin(\theta) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-567796de6904a579b30aad6281860978_l3.png "Rendered by QuickLaTeX.com")
3. Area of the Segment
Now, we can find the area of the segment by subtracting the area of the triangle from the area of the sector:
![\[ A = A_{\text{sector}} - A_{\text{triangle}} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-91f0fd00a9b77eae6f8136b9101116ad_l3.png "Rendered by QuickLaTeX.com")
Substituting the formulas we derived:
![\[ A = \frac{1}{2} r^2 \theta - \frac{1}{2} r^2 \sin(\theta) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-392f8ad40131aa13946b35aa79ea4700_l3.png "Rendered by QuickLaTeX.com")
Factoring out 
:
This gives us the final formula for the area of a segment of a circle.
Example Calculation
To illustrate the application of the area formula, let’s calculate the area of a segment of a circle with a radius of 
units and a central angle of 
.
Step-by-Step Calculation
1. Convert the Angle to Radians:
Since the formula requires the angle in radians, we convert to radians:
![\[ \theta = 60^\circ \times \frac{\pi}{180^\circ} = \frac{\pi}{3} \text{ radians} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-f60b80d5f45a3332b51dbe40308920ea_l3.png "Rendered by QuickLaTeX.com")
2. Identify the Radius:
![\[ r = 10 \text{ units} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-e9be2a7837509296cd155a96cae3c9bd_l3.png "Rendered by QuickLaTeX.com")
3. Calculate the Area of the Segment:
Using the formula:
Substitute and :
![\[ A = \frac{10^2}{2} \left( \frac{\pi}{3} - \sin\left(\frac{\pi}{3}\right) \right) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-fb0e48a622a449e5e825cf109f05d654_l3.png "Rendered by QuickLaTeX.com")
4. Calculate 
:
The sine of (or 
radians) is:
![\[ \sin\left(\frac{\pi}{3}\right) = \frac{\sqrt{3}}{2} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-50ab5df497827dc65ea7cedaf91538fc_l3.png "Rendered by QuickLaTeX.com")
5. Substituting Values:
Now substitute back into the area formula:
![\[ A = \frac{100}{2} \left( \frac{\pi}{3} - \frac{\sqrt{3}}{2} \right) = 50 \left( \frac{\pi}{3} - \frac{\sqrt{3}}{2} \right) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-6780ed2bbdda3cf4d9ab2405725af12f_l3.png "Rendered by QuickLaTeX.com")
6. Final Calculation:
To get a numerical approximation, we can use 
:
![\[ A \approx 50 \left( \frac{3.14}{3} - \frac{\sqrt{3}}{2} \right) \approx 50 \left( 1.047 - 0.866 \right) \approx 50 \times 0.181 \approx 9.05 \text{ square units} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-3a16a2b172d71c81369ab4c459931fd5_l3.png "Rendered by QuickLaTeX.com")
Illustrative Explanation of the Calculation
In this example, we found that the area of the segment of a circle with a radius of units and a central angle of is approximately 
square units. This means that if you were to cover the area of the segment with a material, you would need about square units of that material.
Applications of the Area of a Segment of a Circle
Understanding the area of a segment of a circle has numerous practical applications across various fields:
1. Engineering
In engineering, segments of circles are often used in the design of arches, bridges, and other structures. Calculating the area helps engineers determine material requirements and structural integrity.
2. Architecture
Architects use segments of circles in the design of domes, windows, and other architectural features. Understanding the area is essential for aesthetic and functional considerations.
3. Physics
In physics, the area of a segment of a circle can be relevant in problems involving circular motion, wave patterns, and optics. Understanding the geometry of segments aids in analyzing these phenomena.
4. Geography
In geography, segments of circles can represent land areas, such as sectors of circular fields or plots of land. Calculating the area helps in land use planning and resource management.
5. Art and Design
In art and design, segments of circles are often used in creating patterns, logos, and other visual elements. Understanding the area helps artists and designers create balanced and harmonious compositions.
Conclusion
The area of a segment of a circle is a fundamental concept in geometry that has wide-ranging applications in various fields. The formula provides a straightforward way to calculate the area based on the radius and the angle subtended by the chord. Through the derivation of the formula and the example calculation, we gain a deeper understanding of the relationship between the dimensions of the circle and the area of the segment. As we continue to explore the world of geometry and its applications, the concept of the area of a segment of a circle will remain an essential tool for solving problems and understanding the properties of circular shapes. Whether in engineering, architecture, physics, or art, the segment of a circle plays a vital role in our understanding of shapes and their applications in the real world.