Understanding Linear Velocity: A Comprehensive Overview

Linear velocity is a fundamental concept in physics and engineering that describes the rate at which an object moves along a straight path. It is a vector quantity, meaning it has both magnitude and direction, and is essential for understanding motion in various contexts, from everyday life to complex mechanical systems. This article will provide a detailed exploration of linear velocity, including its definition, mathematical formulation, units, applications, and illustrative explanations to enhance understanding.

1. Definition of Linear Velocity

Linear velocity is defined as the rate of change of an object’s position with respect to time. It indicates how fast an object is moving in a specific direction. Mathematically, linear velocity ( $v$ ) can be expressed as:

$v = \frac{d}{t}$

Where:

$v$ is the linear velocity,
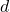$d$ is the displacement (the straight-line distance from the initial position to the final position),
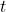$t$ is the time taken to cover that displacement.

Illustrative Explanation: Imagine a car traveling from point A to point B. If the car covers a distance of 100 meters in 5 seconds, the linear velocity can be calculated as follows:

$v = \frac{100 \, \text{meters}}{5 \, \text{seconds}} = 20 \, \text{m/s}$

This means the car is moving at a speed of 20 meters per second in the direction from A to B.

2. Magnitude and Direction of Linear Velocity

A. Magnitude

The magnitude of linear velocity refers to the speed of the object, which is a scalar quantity. It indicates how fast the object is moving, regardless of its direction. The magnitude is often expressed in units such as meters per second (m/s), kilometers per hour (km/h), or miles per hour (mph).

Illustrative Explanation: Consider a runner on a track. If the runner completes a lap of 400 meters in 50 seconds, the magnitude of their linear velocity is:

$v = \frac{400 \, \text{meters}}{50 \, \text{seconds}} = 8 \, \text{m/s}$

This tells us how fast the runner is moving, but not the direction.

B. Direction

The direction of linear velocity is crucial because it indicates the path along which the object is moving. Since linear velocity is a vector quantity, it is essential to specify the direction along with the magnitude. Directions can be expressed in terms of angles, compass directions (north, south, east, west), or coordinate systems (positive x-axis, negative y-axis, etc.).

Illustrative Explanation: If the same runner is moving around the track in a clockwise direction, we can say their linear velocity is 8 m/s to the right (if they are on the straight part of the track). This directional information is vital for understanding the runner’s motion in a two-dimensional space.

3. Units of Linear Velocity

Linear velocity can be expressed in various units, depending on the context. The most common units include:

A. Meters per Second (m/s)

The SI unit for linear velocity is meters per second. It is widely used in scientific contexts and provides a clear understanding of how far an object travels in one second.

Illustrative Explanation: If a bicycle travels 15 meters in 3 seconds, its linear velocity can be calculated as:

$v = \frac{15 \, \text{meters}}{3 \, \text{seconds}} = 5 \, \text{m/s}$

This means the bicycle is moving at a speed of 5 meters per second.

B. Kilometers per Hour (km/h)

Kilometers per hour is commonly used in everyday contexts, especially for vehicles. To convert from meters per second to kilometers per hour, multiply by 3.6.

Illustrative Explanation: If a car is traveling at 20 m/s, its speed in kilometers per hour can be calculated as:

$v = 20 \, \text{m/s} \times 3.6 = 72 \, \text{km/h}$

This conversion helps drivers understand speed limits and travel times more intuitively.

C. Miles per Hour (mph)

Miles per hour is primarily used in the United States and the United Kingdom for road speeds. To convert from meters per second to miles per hour, multiply by approximately 2.23694.

Illustrative Explanation: If a train is moving at 30 m/s, its speed in miles per hour can be calculated as:

$v = 30 \, \text{m/s} \times 2.23694 \approx 67.1 \, \text{mph}$

This conversion is useful for understanding travel speeds in regions that use the imperial system.

4. Applications of Linear Velocity

Linear velocity has numerous applications across various fields, including:

A. Transportation

In transportation, linear velocity is crucial for determining travel times, fuel efficiency, and safety. Understanding the speed of vehicles helps in planning routes and ensuring compliance with speed limits.

Illustrative Explanation: If a bus travels at a linear velocity of 60 km/h, you can estimate how long it will take to reach a destination 120 kilometers away:

$\text{Time} = \frac{120 \, \text{km}}{60 \, \text{km/h}} = 2 \, \text{hours}$

This calculation helps passengers plan their journeys effectively.

B. Sports and Athletics

In sports, linear velocity is essential for analyzing performance. Coaches and athletes use linear velocity to improve techniques, optimize training, and enhance overall performance.

Illustrative Explanation: A sprinter aiming to improve their time in a 100-meter dash can track their linear velocity during practice. If they complete the distance in 10 seconds, their linear velocity is:

$v = \frac{100 \, \text{meters}}{10 \, \text{seconds}} = 10 \, \text{m/s}$

By monitoring this velocity, the athlete can adjust their training regimen to enhance speed.

C. Physics and Engineering

In physics and engineering, linear velocity is fundamental for analyzing motion, designing mechanical systems, and understanding dynamics. It is used in calculations involving forces, energy, and momentum.

Illustrative Explanation: In a roller coaster design, engineers must calculate the linear velocity of the cars at various points along the track to ensure safety and performance. If a car descends a hill and reaches a speed of 15 m/s at the bottom, engineers can assess the forces acting on the riders and the structural integrity of the track.

5. Factors Affecting Linear Velocity

Several factors can influence linear velocity, including:

A. Mass of the Object

While mass does not directly affect linear velocity, it can influence the acceleration of an object when a force is applied, according to Newton’s second law of motion ( $F = ma$ ). A heavier object may require more force to achieve the same linear velocity as a lighter object.

Illustrative Explanation: Imagine two cars, one weighing 1,000 kg and the other 500 kg. If both cars are subjected to the same force, the lighter car will accelerate faster and reach a higher linear velocity more quickly than the heavier car.

B. Friction and Resistance

Friction and air resistance can impede the motion of an object, affecting its linear velocity. Higher friction or resistance results in lower linear velocity for a given force.

Illustrative Explanation: Consider a sled sliding down a snowy hill. If the snow is smooth, the sled will move quickly (high linear velocity). However, if the snow is rough or icy, friction will slow the sled down, reducing its linear velocity.

C. Incline and Gravity

The angle of an incline can affect the linear velocity of an object moving down the slope. A steeper incline results in a greater component of gravitational force acting to accelerate the object.

Illustrative Explanation: Imagine a ball rolling down a ramp. If the ramp is steep, the ball will accelerate quickly and achieve a higher linear velocity at the bottom. Conversely, a gentle slope will result in a slower linear velocity.

6. Conclusion

In summary, linear velocity is a fundamental concept that describes the rate of motion of an object along a straight path. It is a vector quantity characterized by both magnitude and direction, and it plays a crucial role in various applications, from transportation to sports and engineering. Understanding linear velocity allows us to analyze motion, optimize performance, and make informed decisions in everyday life. By grasping the principles of linear velocity, we can better appreciate the dynamics of motion and its implications in the world around us.

Blog.Pengayaan.Com