Understanding the Area of an Equilateral Triangle: A Comprehensive Guide

The equilateral triangle is a fundamental geometric shape characterized by its three equal sides and three equal angles, each measuring 60 degrees. This unique property makes the equilateral triangle a subject of interest in various fields, including mathematics, architecture, and art. One of the key aspects of studying triangles is understanding how to calculate their area. This article will provide a detailed exploration of the area of an equilateral triangle, including its definition, derivation of the area formula, various methods of calculation, and illustrative examples to enhance comprehension.

Definition of an Equilateral Triangle

An equilateral triangle is defined as a triangle in which all three sides are of equal length. Let’s denote the length of each side as $s$ . Due to the symmetry of the equilateral triangle, the height (or altitude) can be calculated using the properties of right triangles formed by dropping a perpendicular from one vertex to the opposite side.

Derivation of the Area Formula

The area $A$ of any triangle can be calculated using the formula:

$A = \frac{1}{2} \times \text{base} \times \text{height}$

In the case of an equilateral triangle, we can derive the area formula by first determining the height. When we drop a perpendicular from one vertex to the midpoint of the opposite side, we create two 30-60-90 right triangles.

Step 1: Finding the Height

In a 30-60-90 triangle, the ratios of the lengths of the sides are as follows:

The side opposite the 30-degree angle is 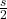$\frac{s}{2}$ (half of the base).
The side opposite the 60-degree angle (the height 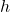$h$ ) can be calculated using the sine function:

$\sin(60^\circ) = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{h}{s}$

Since $\sin(60^\circ) = \frac{\sqrt{3}}{2}$ , we can rearrange the equation to find $h$ :

$h = s \cdot \sin(60^\circ) = s \cdot \frac{\sqrt{3}}{2} = \frac{s\sqrt{3}}{2}$

Step 2: Calculating the Area

Now that we have the height, we can substitute it back into the area formula:

$A = \frac{1}{2} \times s \times h = \frac{1}{2} \times s \times \left(\frac{s\sqrt{3}}{2}\right)$

Simplifying this expression gives:

$A = \frac{1}{2} \times s \times \frac{s\sqrt{3}}{2} = \frac{s^2\sqrt{3}}{4}$

Thus, the area $A$ of an equilateral triangle with side length $s$ is given by the formula:

$A = \frac{s^2\sqrt{3}}{4}$

Alternative Methods to Calculate the Area

While the derived formula is the most straightforward method for calculating the area of an equilateral triangle, there are alternative approaches that can also be employed.

1. Using Heron’s Formula

Heron’s formula allows us to calculate the area of any triangle when the lengths of all three sides are known. For an equilateral triangle, since all sides are equal, we can denote the side length as $s$ . The semi-perimeter $p$ is given by:

$p = \frac{s + s + s}{2} = \frac{3s}{2}$

Using Heron’s formula:

$A = \sqrt{p(p-a)(p-b)(p-c)}$

Substituting $a = b = c = s$ :

$A = \sqrt{\frac{3s}{2} \left(\frac{3s}{2} - s\right) \left(\frac{3s}{2} - s\right) \left(\frac{3s}{2} - s\right)}$

This simplifies to:

$A = \sqrt{\frac{3s}{2} \cdot \frac{s}{2} \cdot \frac{s}{2} \cdot \frac{s}{2}} = \sqrt{\frac{3s^4}{16}} = \frac{s^2\sqrt{3}}{4}$

This confirms the area formula derived earlier.

2. Using Trigonometry

Another method to find the area of an equilateral triangle involves using trigonometric functions. The area can also be expressed in terms of the sine of one of its angles. For an equilateral triangle, the area can be calculated as:

$A = \frac{1}{2}ab\sin(C)$

Where $a$ and $b$ are the lengths of two sides, and $C$ is the included angle. In an equilateral triangle, $a = b = s$ and $C = 60^\circ$ :

$A = \frac{1}{2} \times s \times s \times \sin(60^\circ) = \frac{s^2}{2} \times \frac{\sqrt{3}}{2} = \frac{s^2\sqrt{3}}{4}$

This method provides another verification of the area formula.

Illustrative Examples

To further clarify the concept of calculating the area of an equilateral triangle, let’s consider a few illustrative examples.

Example 1: Area of an Equilateral Triangle with Side Length 6 cm

Given an equilateral triangle with a side length of $s = 6$ cm, we can calculate the area using the formula:

$A = \frac{s^2\sqrt{3}}{4} = \frac{6^2\sqrt{3}}{4} = \frac{36\sqrt{3}}{4} = 9\sqrt{3} \text{ cm}^2$

Calculating the numerical value:

$A \approx 9 \times 1.732 = 15.588 \text{ cm}^2$

Thus, the area of the triangle is approximately $15.59 \text{ cm}^2$ .

Example 2: Area of an Equilateral Triangle with Side Length 10 m

For an equilateral triangle with a side length of $s = 10$ m, we can again use the area formula:

$A = \frac{s^2\sqrt{3}}{4} = \frac{10^2\sqrt{3}}{4} = \frac{100\sqrt{3}}{4} = 25\sqrt{3} \text{ m}^2$

Calculating the numerical value:

$A \approx 25 \times 1.732 = 43.3 \text{ m}^2$

Thus, the area of the triangle is approximately $43.3 \text{ m}^2$ .

Conclusion

In conclusion, the area of an equilateral triangle is a fundamental concept in geometry that can be calculated using various methods, including the derived formula $A = \frac{s^2\sqrt{3}}{4}$ , Heron’s formula, and trigonometric functions. Understanding how to derive and apply these formulas is essential for solving problems related to equilateral triangles in mathematics and its applications in fields such as architecture, engineering, and design. Through detailed explanations and illustrative examples, we can appreciate the beauty and utility of the equilateral triangle in both theoretical and practical contexts.

Blog.Pengayaan.Com