Linear Differential Equations: A Comprehensive Guide

Linear differential equations are a fundamental topic in mathematics, particularly in the fields of engineering, physics, and applied mathematics. They describe a wide range of phenomena, from simple harmonic motion to complex systems in control theory. This article aims to provide a detailed exploration of linear differential equations, including their definitions, classifications, methods of solution, and illustrative explanations to enhance understanding.

1. Definition of Linear Differential Equations

A differential equation is an equation that involves an unknown function and its derivatives. A linear differential equation is a specific type of differential equation in which the unknown function and its derivatives appear linearly, meaning they are not multiplied together or raised to any power other than one.

General Form

The general form of a linear differential equation of order $n$ can be expressed as:

$a_n(x) \frac{d^n y}{dx^n} + a_{n-1}(x) \frac{d^{n-1} y}{dx^{n-1}} + \ldots + a_1(x) \frac{dy}{dx} + a_0(x) y = g(x)$

Where:

$y$ is the unknown function of $x$ .
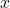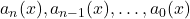$a_n(x), a_{n-1}(x), \ldots, a_0(x)$ are functions of 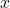$x$ (coefficients).
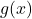$g(x)$ is a known function of 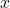$x$ (the non-homogeneous term).

Illustrative Explanation:

Consider the first-order linear differential equation:

$\frac{dy}{dx} + p(x) y = g(x)$

Here, $p(x)$ is a function of $x$ , and $g(x)$ is a known function. The equation is linear because $y$ and its derivative $\frac{dy}{dx}$ appear to the first power and are not multiplied together.

2. Classification of Linear Differential Equations

Linear differential equations can be classified based on their order and whether they are homogeneous or non-homogeneous.

A. Order of the Differential Equation

The order of a differential equation is determined by the highest derivative present in the equation. For example:

A first-order linear differential equation involves the first derivative $\frac{dy}{dx}$ .
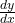A second-order linear differential equation involves the second derivative $\frac{d^2y}{dx^2}$ .

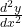B. Homogeneous vs. Non-Homogeneous

A homogeneous linear differential equation is one where 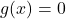$g(x) = 0$ . For example:

$\frac{dy}{dx} + p(x) y = 0$

A non-homogeneous linear differential equation has a non-zero 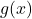$g(x)$ . For example:

$\frac{dy}{dx} + p(x) y = g(x)$

Illustrative Explanation:

For the equation $\frac{dy}{dx} + 2y = 0$ , it is homogeneous because the right side is zero. Conversely, the equation $\frac{dy}{dx} + 2y = 3$ is non-homogeneous because the right side is a constant.

3. Methods of Solving Linear Differential Equations

A. First-Order Linear Differential Equations

To solve a first-order linear differential equation of the form:

$\frac{dy}{dx} + p(x) y = g(x)$

1. Find the Integrating Factor:
The integrating factor $\mu(x)$ is given by:

$\mu(x) = e^{\int p(x) \, dx}$

2. Multiply the entire equation by the integrating factor:
This transforms the left side into the derivative of a product:

$\mu(x) \frac{dy}{dx} + \mu(x) p(x) y = \mu(x) g(x)$

3. Integrate both sides:
After multiplying, the left side can be integrated directly:

$\frac{d}{dx}[\mu(x) y] = \mu(x) g(x)$

Integrate both sides with respect to $x$ :

$\mu(x) y = \int \mu(x) g(x) \, dx + C$

Where $C$ is the constant of integration.

4. Solve for $y$ :
Finally, solve for $y$ :

$y = \frac{1}{\mu(x)} \left( \int \mu(x) g(x) \, dx + C \right)$

Illustrative Example:

Consider the equation:

$\frac{dy}{dx} + 2y = 3$

1. Integrating Factor:
Here, $p(x) = 2$ :

$\mu(x) = e^{\int 2 \, dx} = e^{2x}$

2. Multiply by Integrating Factor:

$e^{2x} \frac{dy}{dx} + 2e^{2x} y = 3e^{2x}$

3. Integrate:

$\frac{d}{dx}[e^{2x} y] = 3e^{2x}$

Integrating both sides gives:

$e^{2x} y = \frac{3}{2} e^{2x} + C$

4. Solve for $y$ :

$y = \frac{3}{2} + Ce^{-2x}$

B. Higher-Order Linear Differential Equations

For higher-order linear differential equations, the approach can vary based on whether the equation is homogeneous or non-homogeneous.

1. Homogeneous Linear Differential Equations

A homogeneous linear differential equation of order $n$ can be expressed as:

$a_n \frac{d^n y}{dx^n} + a_{n-1} \frac{d^{n-1} y}{dx^{n-1}} + \ldots + a_1 \frac{dy}{dx} + a_0 y = 0$

To solve this, we assume a solution of the form $y = e^{rx}$ , where $r$ is a constant. Substituting this into the equation leads to the characteristic equation:

$a_n r^n + a_{n-1} r^{n-1} + \ldots + a_1 r + a_0 = 0$

The roots of this polynomial provide the general solution, which can be a combination of exponential functions, sine, and cosine functions depending on the nature of the roots (real and distinct, real and repeated, or complex).

Illustrative Example:

Consider the second-order homogeneous equation:

$y'' - 3y' + 2y = 0$

1. Characteristic Equation:

$r^2 - 3r + 2 = 0$

Factoring gives:

$(r - 1)(r - 2) = 0 \quad \Rightarrow \quad r = 1, 2$

2. General Solution:

The general solution is:

$y = C_1 e^{x} + C_2 e^{2x}$

2. Non-Homogeneous Linear Differential Equations

For a non-homogeneous linear differential equation, the solution is the sum of the complementary solution (solution to the homogeneous equation) and a particular solution.

1. Find the Complementary Solution:
Solve the associated homogeneous equation as described above.

2. Find a Particular Solution:
Use methods such as undetermined coefficients or variation of parameters to find a particular solution $y_p$ .

3. General Solution:
The general solution is given by:

$y = y_c + y_p$

Illustrative Example:

Consider the non-homogeneous equation:

$y'' - 3y' + 2y = e^{x}$

1. Complementary Solution:
From the previous example, the complementary solution is:

$y_c = C_1 e^{x} + C_2 e^{2x}$

2. Particular Solution:
Assume a particular solution of the form $y_p = Ae^{x}$ . Substituting into the equation and solving for $A$ gives:

$y_p = \frac{1}{2} e^{x}$

3. General Solution:

$y = C_1 e^{x} + C_2 e^{2x} + \frac{1}{2} e^{x} = \left(C_1 + \frac{1}{2}\right)e^{x} + C_2 e^{2x}$

4. Applications of Linear Differential Equations

Linear differential equations have numerous applications across various fields:

A. Physics

In physics, linear differential equations model systems such as harmonic oscillators, electrical circuits, and wave propagation. For example, the motion of a mass-spring system can be described by a second-order linear differential equation.

B. Engineering

In engineering, linear differential equations are used in control systems, signal processing, and structural analysis. They help in designing systems that respond predictably to inputs.

C. Economics

In economics, linear differential equations can model growth rates, investment dynamics, and market equilibrium. They provide insights into how economic variables change over time.

D. Biology

In biology, these equations can describe population dynamics, the spread of diseases, and the growth of organisms. They help in understanding how populations evolve under various conditions.

5. Conclusion

Linear differential equations are a vital part of mathematical theory and practice, providing tools to model and analyze a wide range of real-world phenomena. By understanding their definitions, classifications, and methods of solution, one can effectively tackle problems in various fields, from engineering to economics.

Key Takeaways:

Linear differential equations involve unknown functions and their derivatives in a linear form.
They can be classified by order and whether they are homogeneous or non-homogeneous.
Solutions can be found using methods such as integrating factors for first-order equations and characteristic equations for higher-order equations.
Applications span multiple disciplines, highlighting the importance of linear differential equations in understanding and solving complex problems.

By mastering linear differential equations, individuals can enhance their analytical skills and apply mathematical concepts to real-world situations, making informed decisions based on quantitative analysis.

Blog.Pengayaan.Com

Linear Differential Equations: A Comprehensive Guide

1. Definition of Linear Differential Equations

General Form

Illustrative Explanation:

2. Classification of Linear Differential Equations

A. Order of the Differential Equation

B. Homogeneous vs. Non-Homogeneous

Illustrative Explanation:

3. Methods of Solving Linear Differential Equations

A. First-Order Linear Differential Equations

Illustrative Example:

B. Higher-Order Linear Differential Equations

1. Homogeneous Linear Differential Equations

Illustrative Example:

2. Non-Homogeneous Linear Differential Equations

Illustrative Example:

4. Applications of Linear Differential Equations

A. Physics

B. Engineering

C. Economics

D. Biology

5. Conclusion

Key Takeaways:

Leave a Reply Cancel reply