Understanding the Unit of Torque: A Comprehensive Exploration

Torque is a fundamental concept in physics and engineering, representing the rotational force applied to an object. It plays a crucial role in various applications, from simple mechanical systems to complex machinery. Understanding the unit of torque is essential for engineers, mechanics, and anyone involved in the design and analysis of rotating systems. This article will provide an in-depth examination of torque, its definition, the units used to measure it, the relationship between torque and other physical quantities, and illustrative explanations to enhance understanding.

1. Definition of Torque

Torque, often denoted by the Greek letter tau ( $\tau$ ), is defined as the measure of the rotational force applied to an object about a specific axis. It is the product of the force applied and the distance from the axis of rotation to the point where the force is applied, known as the moment arm or lever arm. Mathematically, torque can be expressed as:

$\tau = r \times F$

where:

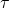$\tau$ is the torque (in newton-meters, N·m),
$r$ is the distance from the axis of rotation to the point of force application (in meters, m),
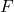$F$ is the force applied (in newtons, N).

Illustrative Explanation: Imagine trying to open a door. The force you apply to the door handle (the force $F$ ) and the distance from the hinges (the axis of rotation) to the handle (the moment arm $r$ ) determine how effectively you can rotate the door. The farther you push from the hinges, the easier it is to open the door, illustrating the concept of torque.

2. Units of Torque

The standard unit of torque in the International System of Units (SI) is the newton-meter (N·m). This unit combines the unit of force (newton) and the unit of distance (meter).

Newton (N): The newton is the SI unit of force, defined as the force required to accelerate a one-kilogram mass by one meter per second squared (1 N = 1 kg·m/s²).
Meter (m): The meter is the SI unit of length, representing the distance traveled by light in a vacuum in 1/299,792,458 seconds.

Thus, when we say that torque is measured in newton-meters, we are referring to the rotational effect produced by a force applied at a certain distance from the axis of rotation.

Illustrative Explanation: Think of torque as a combination of pushing and distance. If you push a heavy object (force) with your hand at the end of a long lever (distance), the torque you create is a measure of how effectively you can turn that object. The unit of newton-meters captures both the strength of your push and how far from the pivot point you are pushing.

3. Alternative Units of Torque

While the newton-meter is the standard unit of torque, other units are also used in different contexts:

Pound-foot (lb·ft): In the United States, torque is often measured in pound-feet, especially in automotive applications. One pound-foot is the torque resulting from a one-pound force applied at a distance of one foot from the axis of rotation.
Kilogram-meter (kg·m): In some engineering contexts, particularly in Europe, torque may be expressed in kilogram-meters. This unit is derived from the force exerted by a one-kilogram mass under the influence of gravity (approximately 9.81 N) applied at a distance of one meter.

Illustrative Explanation: Imagine you are using a wrench to tighten a bolt. If you are in the U.S., you might hear the torque specified in pound-feet, while in Europe, it might be given in kilogram-meters. Regardless of the unit, the concept remains the same: it measures how effectively you can apply a rotational force.

4. Relationship Between Torque and Other Physical Quantities

Torque is closely related to other physical quantities, particularly angular momentum and rotational motion. Understanding these relationships is crucial for analyzing systems involving rotation.

Angular Momentum: Angular momentum ( 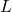$L$ ) is the rotational equivalent of linear momentum and is defined as the product of the moment of inertia ( 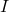$I$ ) and angular velocity ( $\omega$ ):

$L = I \cdot \omega$

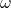Torque is related to angular momentum through the following equation:

$\tau = \frac{dL}{dt}$

This equation states that the torque applied to an object is equal to the rate of change of its angular momentum over time.

Illustrative Explanation: Imagine a spinning figure skater. As they pull their arms in (changing their moment of inertia), they spin faster (increasing angular velocity). The torque they exert by pulling their arms in changes their angular momentum, illustrating the relationship between these concepts.

Rotational Kinematics: Torque is also related to rotational kinematics, which describes the motion of rotating objects. The angular acceleration ( 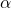$\alpha$ ) of an object is directly proportional to the torque applied and inversely proportional to its moment of inertia:

$\tau = I \cdot \alpha$

This relationship shows that a greater torque will result in a higher angular acceleration, assuming the moment of inertia remains constant.

Illustrative Explanation: Think of a merry-go-round. If you push it harder (increasing torque), it will spin faster (greater angular acceleration). If the merry-go-round is heavier (greater moment of inertia), it will be harder to get it spinning quickly, demonstrating the interplay between torque, angular acceleration, and moment of inertia.

5. Applications of Torque

Torque has numerous practical applications across various fields, including:

Automotive Engineering: Torque is a critical parameter in engine performance, affecting acceleration and the ability to move heavy loads. Torque ratings are often provided for engines to indicate their capability.
Mechanical Systems: In machinery, torque is essential for understanding how forces are transmitted through gears, levers, and other mechanical components. Engineers must calculate torque to ensure that components can withstand the forces applied during operation.
Sports and Fitness: In sports, torque is relevant in activities such as throwing, swinging, and kicking. Athletes often use torque to maximize their performance by optimizing their movements.

Illustrative Explanation: Imagine a car engine. The torque produced by the engine determines how quickly the car can accelerate. If the engine has high torque, it can move the car faster, especially when starting from a stop or climbing a hill. Similarly, in sports, a baseball pitcher uses torque in their arm to throw the ball with maximum speed and distance.

6. Measuring Torque

Torque can be measured using various instruments, including:

Torque Wrenches: These tools are commonly used in automotive and construction applications to apply a specific torque to fasteners. They provide a tactile or audible indication when the desired torque is reached.
Dynamometers: These devices measure torque and power output in engines and motors. They can provide real-time data on how much torque an engine produces at different RPMs (revolutions per minute).
Torque Sensors: These sensors are used in industrial applications to monitor and control torque in machinery. They provide feedback to ensure that components are operating within specified torque limits.

Illustrative Explanation: Think of a torque wrench as a measuring cup for torque. Just as a measuring cup helps you pour the right amount of liquid, a torque wrench helps you apply the correct amount of rotational force to a bolt. When you reach the desired torque, the wrench signals you, ensuring that everything is tightened properly.

Conclusion

The unit of torque is a fundamental concept in physics and engineering, representing the rotational force applied to an object. By exploring its definition, mathematical formulation, alternative units, relationships with other physical quantities, applications, and measurement techniques, we gain a deeper appreciation for its significance in various fields. Torque is not just a theoretical concept; it has practical implications in automotive engineering, mechanical systems, sports, and many other areas. Understanding torque allows engineers and scientists to design and analyze systems effectively, ensuring optimal performance and safety in a wide range of applications. Whether you are tightening a bolt, designing a machine, or analyzing the motion of a rotating object, the concept of torque is essential for understanding the forces at play.

Blog.Pengayaan.Com