Angular acceleration is a fundamental concept in physics and engineering that describes how quickly an object is rotating and how that rotation is changing over time. It is a crucial parameter in the study of rotational motion, which is essential for understanding the dynamics of various systems, from simple mechanical devices to complex machinery and celestial bodies. This article will delve into the definition of angular acceleration, its mathematical formulation, its relationship with other physical quantities, and its applications, providing detailed explanations and illustrative examples to enhance understanding.
What is Angular Acceleration?
Definition
Angular acceleration (
) is defined as the rate of change of angular velocity (
) with respect to time. It quantifies how quickly an object is speeding up or slowing down its rotation. Angular acceleration is a vector quantity, meaning it has both magnitude and direction. The direction of angular acceleration is determined by the direction of the change in angular velocity.
- Illustrative Explanation: Imagine a figure skater spinning. As the skater pulls their arms in, they spin faster, which indicates a positive angular acceleration. Conversely, if the skater extends their arms and slows down, they experience negative angular acceleration (deceleration). The change in their spinning speed over time is what angular acceleration measures.
Units of Angular Acceleration
The SI unit of angular acceleration is radians per second squared (
). This unit indicates how many radians the angular velocity changes per second. For example, an angular acceleration of 
means that the angular velocity increases by 
radians per second for every second that passes.
Mathematical Formulation of Angular Acceleration
Angular acceleration can be mathematically expressed using the following formula:
![\[ \alpha = \frac{\Delta \omega}{\Delta t} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-59dc8fa68d6434f2ddf4500325e24915_l3.png "Rendered by QuickLaTeX.com")
Where:
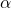- = angular acceleration
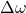= change in angular velocity
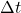= change in time
Example Calculation
Suppose a wheel’s angular velocity changes from 
to 
over a period of 
seconds. The angular acceleration can be calculated as follows:
1. Determine the change in angular velocity:
![\[ \Delta \omega = \omega_f - \omega_i = 20 \, \text{rad/s} - 10 \, \text{rad/s} = 10 \, \text{rad/s} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-968cd09ffcad1fd18ef673dcf3fc658d_l3.png "Rendered by QuickLaTeX.com")
2. Calculate the angular acceleration:
![\[ \alpha = \frac{\Delta \omega}{\Delta t} = \frac{10 \, \text{rad/s}}{5 \, \text{s}} = 2 \, \text{rad/s}^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-2be96eff0370874e7f413559b158020e_l3.png "Rendered by QuickLaTeX.com")
This result indicates that the wheel’s angular velocity increases by 
every second.
Relationship Between Angular Acceleration and Other Quantities
Angular acceleration is closely related to other physical quantities in rotational motion, including torque, moment of inertia, and angular velocity. Understanding these relationships is essential for analyzing rotational dynamics.
1. Torque and Angular Acceleration
Torque (
) is the rotational equivalent of linear force. It is the measure of the force that causes an object to rotate about an axis. The relationship between torque, angular acceleration, and moment of inertia (
) is given by Newton’s second law for rotation:
![\[ \tau = I \alpha \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-ea7a57ac3b04561f8b5e8f2940d97e69_l3.png "Rendered by QuickLaTeX.com")
Where:
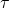- = torque
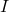- = moment of inertia (a measure of an object’s resistance to changes in its rotational motion)
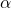- = angular acceleration
- Illustrative Explanation: Consider a door being pushed open. The force applied at the edge of the door creates torque, which causes the door to rotate. If you push harder (increasing torque), the door will accelerate faster (greater angular acceleration). The moment of inertia of the door (how heavy it feels to rotate) also affects how quickly it accelerates.
2. Moment of Inertia
The moment of inertia () is a property of an object that quantifies its resistance to angular acceleration. It depends on the mass distribution of the object relative to the axis of rotation. The greater the moment of inertia, the more torque is required to achieve a given angular acceleration.
- Illustrative Explanation: Imagine two objects: a solid sphere and a hollow sphere of the same mass and radius. If you apply the same torque to both, the solid sphere will accelerate faster than the hollow sphere because its mass is distributed closer to the center, resulting in a lower moment of inertia.
3. Angular Velocity
Angular acceleration is the rate of change of angular velocity. If an object has a constant angular acceleration, its angular velocity can be calculated using the following equation:
![\[ \omega_f = \omega_i + \alpha \Delta t \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-291c613227e65456711aafaa577289b0_l3.png "Rendered by QuickLaTeX.com")
Where:
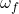= final angular velocity
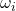= initial angular velocity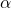- = angular acceleration
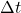- = change in time
- Illustrative Explanation: If a car’s wheels are initially spinning at
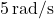and experience an angular acceleration of 
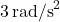for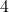 
seconds, the final angular velocity can be calculated as follows:
![\[ \omega_f = 5 \, \text{rad/s} + (3 \, \text{rad/s}^2 \times 4 \, \text{s}) = 5 \, \text{rad/s} + 12 \, \text{rad/s} = 17 \, \text{rad/s} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-b70c8ab77560c14af5db24018b9ce300_l3.png "Rendered by QuickLaTeX.com")
This calculation shows how the angular velocity increases due to the applied angular acceleration.
Applications of Angular Acceleration
Angular acceleration has numerous applications across various fields, including engineering, physics, and everyday life. Some notable applications include:
1. Rotational Motion in Machinery
In mechanical engineering, understanding angular acceleration is crucial for designing and analyzing rotating machinery, such as engines, turbines, and gears. Engineers must consider angular acceleration to ensure that components can withstand the forces generated during operation.
- Illustrative Explanation: Consider a wind turbine. The blades rotate to harness wind energy, and the angular acceleration of the blades affects how quickly they can reach their optimal speed. Engineers must design the turbine to handle the stresses associated with rapid changes in angular acceleration.
2. Sports and Athletics
In sports, athletes often utilize angular acceleration to enhance performance. For example, gymnasts and divers use angular acceleration to control their rotations during flips and twists.
- Illustrative Explanation: Imagine a diver performing a somersault. By tucking their body in, they reduce their moment of inertia, allowing them to spin faster (greater angular acceleration) and complete more rotations before entering the water.
3. Automotive Engineering
In automotive engineering, angular acceleration is essential for understanding the performance of vehicles. The acceleration of wheels affects the vehicle’s speed and handling, and engineers must optimize the design of braking systems to manage angular acceleration effectively.
- Illustrative Explanation: When a driver accelerates a car, the wheels experience angular acceleration. If the driver suddenly applies the brakes, the angular acceleration changes rapidly, affecting the car’s stability. Engineers must design braking systems that can handle these changes safely.
4. Astronomy and Astrophysics
In astronomy, angular acceleration is used to describe the motion of celestial bodies, such as planets and stars. Understanding the angular acceleration of these bodies helps scientists predict their orbits and interactions.
- Illustrative Explanation: Consider a planet orbiting a star. As the planet moves closer to the star, it experiences an increase in angular acceleration due to the stronger gravitational pull. This change in angular acceleration affects the planet’s orbital path and speed.
Conclusion
Angular acceleration is a fundamental concept in the study of rotational motion, providing valuable insights into how objects rotate and how their motion changes over time. By understanding the relationship between angular acceleration, torque, moment of inertia, and angular velocity, we can analyze and predict the behavior of various systems in physics and engineering. Its applications span a wide range of fields, from machinery design to sports performance and celestial mechanics. As we continue to explore the intricacies of motion, angular acceleration will remain a key parameter in our understanding of the physical world.