The refractive index, often denoted as 
, is a fundamental property of materials that describes how light propagates through them. It is defined as the ratio of the speed of light in a vacuum to the speed of light in a given medium. The refractive index is crucial in understanding various optical phenomena, including refraction, reflection, and dispersion. This article will delve into the concept of refractive index, its mathematical formulation, its significance in optics, and its applications in various fields.
Definition of Refractive Index
The refractive index of a medium is mathematically expressed as:
![\[ n = \frac{c}{v} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-8f9e2f4cb58a67965f1c352a0f7479c0_l3.png "Rendered by QuickLaTeX.com")
where:
is the speed of light in a vacuum (approximately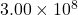 
meters per second),
is the speed of light in the medium.
This equation indicates that the refractive index is a dimensionless number, as it is a ratio of two speeds. The refractive index can also be understood in terms of the wavelength of light in different media, as the speed of light changes depending on the medium through which it travels.
Understanding Refraction
Refraction is the bending of light as it passes from one medium to another with a different refractive index. This bending occurs because light travels at different speeds in different materials. When light enters a medium with a higher refractive index, it slows down and bends towards the normal (an imaginary line perpendicular to the surface at the point of incidence). Conversely, when light exits a medium with a higher refractive index to one with a lower refractive index, it speeds up and bends away from the normal.
Snell’s Law
The relationship between the angles of incidence and refraction is described by Snell’s Law, which states:
![\[ n_1 \sin(\theta_1) = n_2 \sin(\theta_2) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-8b344e79e85a28a48d549870b3c7faf9_l3.png "Rendered by QuickLaTeX.com")
where:
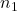and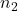 
are the refractive indices of the first and second media, respectively,
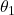is the angle of incidence (the angle between the incident ray and the normal),
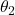is the angle of refraction (the angle between the refracted ray and the normal).
Illustrative Example of Refraction
To illustrate the concept of refraction and the refractive index, consider a beam of light traveling from air (with a refractive index of approximately 1.00) into water (with a refractive index of approximately 1.33).
1. Incident Ray: A light ray strikes the surface of the water at an angle of incidence .
2. Refraction: As the light enters the water, it slows down due to the higher refractive index and bends towards the normal. The angle of refraction can be calculated using Snell’s Law:
![\[ n_{air} \sin(\theta_1) = n_{water} \sin(\theta_2) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-aae2fca4d3f0048d6c4307b1a3173324_l3.png "Rendered by QuickLaTeX.com")
For example, if 
:
![\[ 1.00 \cdot \sin(30^\circ) = 1.33 \cdot \sin(\theta_2) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-83ee01c0c770e17f899d51649e3a161d_l3.png "Rendered by QuickLaTeX.com")
Solving for gives:
![\[ \sin(\theta_2) = \frac{1.00 \cdot 0.5}{1.33} \approx 0.375 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-88e2702470d7eefe98edb9e2f4c94b3f_l3.png "Rendered by QuickLaTeX.com")
Thus, 
.
This example demonstrates how light bends when transitioning between two media with different refractive indices.
Factors Affecting Refractive Index
1. Wavelength of Light: The refractive index of a material can vary with the wavelength of light, a phenomenon known as dispersion. Shorter wavelengths (blue light) typically have a higher refractive index than longer wavelengths (red light). This is why prisms can separate white light into its constituent colors.
2. Temperature: The refractive index can change with temperature, as the density of the medium may vary. For example, heating a glass can decrease its density and, consequently, its refractive index.
3. Composition of the Material: Different materials have different refractive indices based on their molecular structure and density. For instance, diamond has a very high refractive index (approximately 2.42) compared to glass (around 1.5).
Applications of Refractive Index
1. Optical Lenses: The design of lenses for glasses, cameras, and microscopes relies heavily on the refractive index. By selecting materials with specific refractive indices, manufacturers can create lenses that focus light effectively.
2. Fiber Optics: In fiber optic technology, light is transmitted through thin strands of glass or plastic. The refractive index is crucial for ensuring total internal reflection, allowing light to travel long distances with minimal loss.
3. Spectroscopy: The refractive index is used in spectroscopy to analyze the composition of substances. By measuring how light refracts through a sample, scientists can determine its properties and identify its components.
4. Meteorology: The refractive index of air changes with temperature, pressure, and humidity, affecting how light travels through the atmosphere. This is important for understanding phenomena such as mirages and the apparent position of celestial objects.
5. Medical Imaging: Techniques such as optical coherence tomography (OCT) utilize the refractive index to create detailed images of biological tissues, aiding in medical diagnostics.
Measuring Refractive Index
The refractive index can be measured using various methods, including:
1. Refractometers: These instruments measure the angle of refraction when light passes through a sample. The refractive index can be calculated based on the known angle of incidence and the angle of refraction.
2. Critical Angle Method: This method involves measuring the angle at which total internal reflection occurs. The critical angle can be used to calculate the refractive index using Snell’s Law.
3. Interferometry: This technique uses the interference of light waves to measure small changes in the refractive index with high precision.
Conclusion
In conclusion, the refractive index is a fundamental concept in optics that describes how light interacts with different materials. By understanding the refractive index, we can explain and predict various optical phenomena, from the bending of light to the functioning of lenses and fiber optics. The refractive index is influenced by factors such as wavelength, temperature, and material composition, making it a versatile and essential property in both scientific research and practical applications. Whether in designing optical devices, analyzing materials, or studying atmospheric effects, the refractive index plays a crucial role in our understanding of light and its behavior in different media. As technology continues to advance, the importance of refractive index in various fields will only grow, highlighting the need for continued exploration and understanding of this fundamental optical property.