Understanding the Basic Proportionality Theorem: A Comprehensive Guide

The Basic Proportionality Theorem, also known as Thales’ Theorem, is a fundamental concept in geometry that deals with the relationships between the sides of triangles and the segments created by parallel lines intersecting those triangles. This theorem is not only pivotal in the study of geometry but also has practical applications in various fields such as architecture, engineering, and art. This article will provide a detailed exploration of the Basic Proportionality Theorem, including its definition, proof, applications, and illustrative examples to enhance understanding.

Definition of the Basic Proportionality Theorem

The Basic Proportionality Theorem states that if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally. In simpler terms, if a triangle has a line segment parallel to side , intersecting sides and at points and respectively, then the following relationship holds:

   

Where:

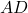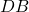• and are segments of side ,
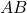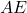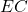• and are segments of side .

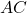This theorem establishes a proportional relationship between the segments created by the intersection of the parallel line with the sides of the triangle.

Visual Representation

To better understand the Basic Proportionality Theorem, consider the following diagram:

“`
     A
    / \
   /   \
  /     \
D--------E
/         \
B———–------C
“`

In this triangle , line segment is drawn parallel to side . According to the theorem, the segments and on side are proportional to the segments and on side .

Proof of the Basic Proportionality Theorem

The proof of the Basic Proportionality Theorem can be established using similar triangles. Here’s a step-by-step breakdown of the proof:

Step 1: Identify Similar Triangles

Since line is parallel to side , triangles and are similar by the Basic Angle-Angle (AA) criterion for similarity. This is because:

• Angle is common to both triangles.
• Angle 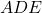is equal to angle (corresponding angles).

Step 2: Set Up Proportions

From the similarity of triangles and , we can set up the following proportion based on the corresponding sides:

   

Step 3: Express the Segments

Since and , we can express the segments in terms of the whole sides:

   

Step 4: Cross-Multiply

Cross-multiplying gives us:

   

Step 5: Rearranging the Equation

This can be rearranged to show that:

   

By simplifying, we find that:

   

Step 6: Final Proportionality

Dividing both sides by gives us the desired proportionality:

   

This completes the proof of the Basic Proportionality Theorem.

Applications of the Basic Proportionality Theorem

The Basic Proportionality Theorem has several important applications in various fields:

1. Geometry: It is used to solve problems involving similar triangles, allowing for the calculation of unknown lengths when certain lengths are known.

2. Construction and Architecture: Architects and engineers use this theorem to create scale models and ensure that proportions are maintained in designs.

3. Art: Artists apply the principles of proportionality to create aesthetically pleasing compositions, ensuring that elements within their work are proportionally balanced.

4. Surveying: In land surveying, the theorem helps in determining distances and areas by establishing proportional relationships between segments.

Illustrative Examples

To further clarify the Basic Proportionality Theorem, let’s consider a few illustrative examples.

Example 1: Finding Unknown Lengths

Suppose we have triangle with cm, cm, and we want to find if cm.

Using the Basic Proportionality Theorem:

   

Substituting the known values:

   

Cross-multiplying gives:

   

   

Dividing both sides by 3:

   

Example 2: Proportional Segments in a Triangle

Consider triangle where cm, cm, and a line segment is drawn parallel to side , dividing into segments cm and cm. We want to find the length of segment .

Using the Basic Proportionality Theorem:

   

Since , we have:

   

This simplifies to:

   

Thus, cm.

Conclusion

In conclusion, the Basic Proportionality Theorem is a fundamental concept in geometry that establishes a proportional relationship between segments created by a line parallel to one side of a triangle. Understanding this theorem is essential for solving various geometric problems and has practical applications in fields such as architecture, engineering, art, and surveying. Through detailed explanations, proofs, and illustrative examples, we can appreciate the significance of the Basic Proportionality Theorem in both theoretical and practical contexts. Whether calculating unknown lengths or applying proportionality in design, this theorem remains a cornerstone of geometric understanding.