Understanding the Perimeter of a Square: A Comprehensive Guide

The perimeter of a square is a fundamental concept in geometry that plays a crucial role in various mathematical applications and real-world scenarios. This article will provide a detailed exploration of the perimeter of a square, including its definition, properties, formula, methods of calculation, and illustrative examples to enhance understanding.

Definition of a Square

A square is a special type of quadrilateral (four-sided polygon) characterized by the following properties:

1. Equal Sides: All four sides of a square are of equal length.
2. Right Angles: Each of the four angles in a square measures 90 degrees.
3. Parallel Sides: Opposite sides of a square are parallel to each other.

Given these properties, a square is a regular polygon, meaning that it is both equilateral (all sides are equal) and equiangular (all angles are equal).

Definition of Perimeter

The perimeter of a geometric shape is defined as the total distance around the shape. It is the sum of the lengths of all the sides of the shape. For a square, since all four sides are equal, the perimeter can be calculated using a simple formula.

Formula for the Perimeter of a Square

The perimeter $P$ of a square can be calculated using the formula:

$P = 4s$

Where:

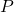$P$ is the perimeter of the square.
$s$ is the length of one side of the square.

This formula arises from the fact that a square has four equal sides, so the perimeter is simply four times the length of one side.

Properties of the Perimeter of a Square

1. Directly Proportional to Side Length: The perimeter of a square is directly proportional to the length of its sides. If the length of a side increases, the perimeter increases proportionally.

2. Units of Measurement: The perimeter is expressed in linear units, such as meters (m), centimeters (cm), inches (in), or feet (ft). The unit of the perimeter will be the same as the unit used for the side length.

3. Constant Ratio: For any square, the ratio of the perimeter to the side length is always constant and equal to 4. This means that if you know the perimeter, you can easily find the side length by rearranging the formula:

$s = \frac{P}{4}$

4. Geometric Interpretation: The perimeter represents the total distance one would travel if walking around the square, making it a practical measure in various applications, such as fencing a yard or framing a picture.

Calculation of the Perimeter of a Square

To calculate the perimeter of a square, follow these steps:

1. Measure the Length of One Side: Use a ruler or measuring tape to determine the length of one side of the square.

2. Apply the Formula: Substitute the measured length into the perimeter formula $P = 4s$ .

3. Perform the Calculation: Multiply the length of the side by 4 to find the perimeter.

Illustrative Example:

Let’s say we have a square with a side length of $s = 5 \, \text{cm}$ .

1. Measure the Side: The length of one side is $5 \, \text{cm}$ .
2. Apply the Formula:

$P = 4s = 4 \times 5 \, \text{cm}$

3. Calculate the Perimeter:

$P = 20 \, \text{cm}$

Thus, the perimeter of the square is $20 \, \text{cm}$ .

Visual Representation of a Square and Its Perimeter

To visualize a square and its perimeter, consider the following diagram:

“`
+—————–+
|      |
|      | s
|      |
+—————–+
“`

In this diagram, the square has four equal sides, each labeled as $s$ . The perimeter $P$ is the total distance around the square, which can be calculated as $P = 4s$ .

Applications of the Perimeter of a Square

The concept of the perimeter of a square has numerous practical applications, including:

1. Fencing: When planning to fence a square garden or yard, knowing the perimeter helps determine how much fencing material is needed.

2. Construction: In construction, calculating the perimeter is essential for determining the amount of materials required for framing, flooring, or roofing.

3. Landscaping: For landscaping projects, the perimeter of a square plot can help in planning the layout of plants, pathways, and other features.

4. Art and Design: In art and design, understanding the perimeter of squares is important for creating balanced and proportionate designs, such as picture frames or tiles.

5. Sports: In sports, the perimeter of square fields or courts can be used to determine the distance around the playing area, which is important for setting up boundaries and markings.

Conclusion

In conclusion, the perimeter of a square is a fundamental concept in geometry characterized by its simplicity and direct relationship to the length of the sides. Understanding how to calculate the perimeter using the formula $P = 4s$ is essential for solving various mathematical problems and for practical applications in fields such as construction, landscaping, and design. Through detailed explanations and illustrative examples, we can appreciate the significance of the perimeter of a square in both theoretical and practical contexts, showcasing its importance in the broader landscape of mathematics. Whether measuring a garden, planning a construction project, or designing a piece of art, the perimeter of a square remains a cornerstone of geometric understanding and application.

Blog.Pengayaan.Com