Coefficient of Linear Expansion: A Comprehensive Exploration

The coefficient of linear expansion is a fundamental concept in materials science and engineering that describes how the size of an object changes with temperature. As materials are heated, they tend to expand, and this expansion can be quantified using the coefficient of linear expansion. Understanding this concept is crucial for various applications, including construction, manufacturing, and thermodynamics. This article aims to provide an exhaustive overview of the coefficient of linear expansion, detailing its definition, mathematical formulation, factors affecting it, and practical applications, along with illustrative explanations of each concept.

Understanding Linear Expansion

1. Definition of Linear Expansion

Linear expansion refers to the change in length of a material as a result of a change in temperature. When a material is heated, its particles gain energy and move more vigorously, causing the material to expand. The coefficient of linear expansion ( $\alpha$ ) quantifies this change in length per unit length per degree change in temperature.

The formula for linear expansion can be expressed as:

$\Delta L = L_0 \cdot \alpha \cdot \Delta T$

Where:

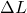$\Delta L$ is the change in length,
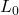$L_0$ is the original length of the material,
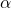$\alpha$ is the coefficient of linear expansion,
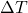$\Delta T$ is the change in temperature (in degrees Celsius or Kelvin).
Illustrative Explanation: Imagine a metal rod that is initially 1 meter long. If the temperature of the rod increases by 100 degrees Celsius and the coefficient of linear expansion for the metal is 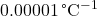$0.00001 \, \text{°C}^{-1}$ , the change in length can be calculated as follows:

$\Delta L = 1 \, \text{m} \cdot 0.00001 \, \text{°C}^{-1} \cdot 100 \, \text{°C} = 0.001 \, \text{m} = 1 \, \text{mm}$

This means the rod will expand by 1 millimeter when heated by 100 degrees Celsius.

2. Understanding the Coefficient of Linear Expansion

The coefficient of linear expansion ( $\alpha$ ) is a material-specific property that indicates how much a material will expand per unit length for each degree of temperature increase. It is typically expressed in units of $\text{°C}^{-1}$ or $\text{K}^{-1}$ .

Illustrative Explanation: Different materials have different coefficients of linear expansion. For example, metals like aluminum have a higher coefficient of linear expansion (approximately 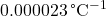$0.000023 \, \text{°C}^{-1}$ ) compared to glass (approximately 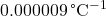$0.000009 \, \text{°C}^{-1}$ ). This means that for the same temperature change, aluminum will expand more than glass. If both materials are subjected to the same temperature increase, the aluminum rod will elongate more than the glass rod.

Factors Affecting the Coefficient of Linear Expansion

3. Material Composition

The coefficient of linear expansion varies significantly among different materials due to their atomic structure and bonding. Generally, metals have higher coefficients of linear expansion compared to ceramics and polymers.

Illustrative Explanation: Consider a steel beam and a concrete column in a building. When exposed to heat, the steel beam will expand more than the concrete column due to its higher coefficient of linear expansion. This difference in expansion can lead to structural issues if not properly accounted for in the design.

4. Temperature Range

The coefficient of linear expansion can also change with temperature. For many materials, the coefficient is relatively constant over small temperature ranges, but it may vary at higher temperatures or extreme conditions.

Illustrative Explanation: Imagine a metal rod that expands uniformly when heated from room temperature to 100 degrees Celsius. However, if the temperature is increased to 500 degrees Celsius, the atomic vibrations within the metal may change, leading to a different expansion rate. Engineers must consider these variations when designing components that will experience significant temperature changes.

5. Phase of the Material

The phase of a material (solid, liquid, or gas) can influence its coefficient of linear expansion. Generally, solids have lower coefficients compared to liquids and gases, which can expand significantly with temperature changes.

Illustrative Explanation: When water is heated, it expands more than most solids. For instance, when water is heated from 0 to 100 degrees Celsius, it expands significantly, which is why boiling water can overflow from a pot. In contrast, a metal rod may only expand a few millimeters under the same temperature change.

Practical Applications of the Coefficient of Linear Expansion

6. Construction and Engineering

In construction and engineering, understanding the coefficient of linear expansion is crucial for designing structures that can withstand temperature fluctuations. Materials must be selected and joined in a way that accommodates expansion and contraction.

Illustrative Explanation: When constructing bridges, engineers must account for the expansion of metal components due to temperature changes. Expansion joints are often incorporated into the design to allow for the movement of materials without causing structural damage. For example, a bridge made of steel will expand on hot days, and the expansion joints will allow it to do so without buckling.

7. Manufacturing Processes

In manufacturing, the coefficient of linear expansion is important for processes such as machining, welding, and assembly. Understanding how materials will behave under temperature changes helps prevent defects and ensures product quality.

Illustrative Explanation: When machining metal parts, manufacturers must consider the thermal expansion of the material. If a metal part is machined at room temperature and then heated during operation, it may expand and cause tight tolerances to become loose, leading to malfunction. Proper planning and adjustments are necessary to maintain the integrity of the final product.

8. Thermal Stress Analysis

In thermal stress analysis, the coefficient of linear expansion is used to predict how materials will respond to temperature changes. This analysis is critical in applications where materials are subjected to varying temperatures, such as in aerospace and automotive industries.

Illustrative Explanation: In an aircraft engine, components experience extreme temperature variations during operation. Engineers use the coefficient of linear expansion to model how different materials will expand and contract, ensuring that the components can withstand thermal stresses without failure.

Conclusion

In conclusion, the coefficient of linear expansion is a vital concept in materials science and engineering that quantifies how materials change in length with temperature. Understanding this coefficient, along with the factors that influence it, is essential for various applications, including construction, manufacturing, and thermal stress analysis. By considering the coefficient of linear expansion, engineers and designers can create structures and components that are resilient to temperature fluctuations, ensuring safety and functionality in a wide range of environments. As technology continues to advance, the importance of understanding material properties like the coefficient of linear expansion will remain critical in the development of innovative solutions across industries.

Blog.Pengayaan.Com