Understanding Spherical Mirrors: A Comprehensive Exploration

Spherical mirrors are reflective surfaces that are shaped like a portion of a sphere. They are widely used in various applications, from everyday household items to complex optical instruments. This article will provide an in-depth examination of spherical mirrors, covering their definition, types, characteristics, formation of images, mathematical formulations, examples, and applications, along with illustrative explanations to enhance understanding.

1. Definition of Spherical Mirrors

A spherical mirror is a mirror with a polished, reflective surface that is part of a hollow sphere of glass or plastic. The reflective side of the mirror can either face inward or outward, leading to two distinct types of spherical mirrors: concave mirrors and convex mirrors.

Concave Mirror: A concave mirror has a reflective surface that curves inward, resembling a portion of the interior of a sphere. This type of mirror can converge light rays that strike its surface.
Convex Mirror: A convex mirror has a reflective surface that bulges outward, resembling a portion of the exterior of a sphere. This type of mirror diverges light rays that strike its surface.

Illustrative Explanation: Imagine a soup bowl. The inside of the bowl represents a concave mirror, where the reflective surface curves inward. Conversely, the outside of the bowl represents a convex mirror, where the surface bulges outward.

2. Types of Spherical Mirrors

As mentioned, there are two primary types of spherical mirrors, each with distinct properties and applications:

Concave Mirrors: These mirrors are used to focus light and are commonly found in applications such as makeup mirrors, shaving mirrors, and telescopes. When parallel rays of light strike a concave mirror, they converge at a point known as the focal point.
Convex Mirrors: These mirrors are used for wide-angle viewing and are commonly found in vehicle side mirrors, security mirrors, and in stores to monitor large areas. When parallel rays of light strike a convex mirror, they diverge, and the extensions of these rays appear to originate from a virtual focal point behind the mirror.

Illustrative Explanation: Consider a makeup mirror that is slightly curved inward (concave). When you look into it, your reflection appears larger and clearer because the mirror focuses the light onto your face. In contrast, a convex mirror, like those used on the sides of cars, allows drivers to see a wider area behind them, although objects appear smaller.

3. Characteristics of Spherical Mirrors

Spherical mirrors possess several key characteristics that define their behavior and applications:

Focal Point (F): The focal point is the point where parallel rays of light either converge (in concave mirrors) or appear to diverge from (in convex mirrors). The distance from the mirror’s surface to the focal point is known as the focal length ( $f$ ).
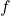Center of Curvature (C): The center of curvature is the center of the sphere from which the mirror is derived. It is located at a distance equal to twice the focal length from the mirror’s surface.
Principal Axis: The principal axis is an imaginary line that passes through the center of curvature and the focal point, extending in both directions. It serves as a reference line for measuring distances and angles.
Radius of Curvature (R): The radius of curvature is the radius of the sphere from which the mirror is made. It is related to the focal length by the equation:

$R = 2f$

Where $R$ is the radius of curvature and $f$ is the focal length.

Illustrative Explanation: Visualize a flashlight beam shining parallel to the principal axis of a concave mirror. The light rays converge at the focal point, creating a bright spot. In contrast, if you shine a flashlight parallel to the principal axis of a convex mirror, the light rays appear to diverge, creating a virtual focal point behind the mirror.

4. Formation of Images by Spherical Mirrors

Spherical mirrors can form images of objects placed in front of them. The characteristics of the images formed depend on the type of mirror and the position of the object relative to the focal point and center of curvature.

Concave Mirrors: The image formed by a concave mirror can be real or virtual, depending on the object’s position:
Object beyond C: The image is real, inverted, and smaller than the object.
Object at C: The image is real, inverted, and the same size as the object.
Object between C and F: The image is real, inverted, and larger than the object.
Object at F: The image is formed at infinity (theoretically).
Object between F and the mirror: The image is virtual, upright, and larger than the object.
Convex Mirrors: The image formed by a convex mirror is always virtual, upright, and smaller than the object, regardless of the object’s position.

Illustrative Explanation: Imagine holding a flashlight in front of a concave mirror. If you position the flashlight close to the mirror (between the focal point and the mirror), the light reflects and creates a larger, upright image of the flashlight. If you move the flashlight further away (beyond the center of curvature), the image becomes smaller and inverted. In contrast, if you use a convex mirror, the flashlight will always appear smaller and upright, regardless of its distance from the mirror.

5. Mathematical Formulation of Spherical Mirrors

The behavior of spherical mirrors can be described mathematically using the mirror formula and magnification formula:

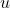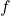Mirror Formula: The relationship between the object distance ( $u$ ), image distance ( $v$ ), and focal length ( $f$ ) is given by the mirror formula:

$\frac{1}{f} = \frac{1}{v} + \frac{1}{u}$

Where:

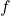$f$ is the focal length (positive for concave mirrors and negative for convex mirrors).
$v$ is the image distance (positive for real images and negative for virtual images).
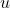$u$ is the object distance (always negative in the mirror convention).
Magnification Formula: The magnification ( 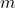$m$ ) of the image is given by the formula:

$m = \frac{h'}{h} = -\frac{v}{u}$

Where:

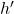$h'$ is the height of the image.
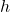$h$ is the height of the object.
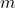$m$ is positive for upright images and negative for inverted images.

Illustrative Explanation: Suppose you have a concave mirror with a focal length of 10 cm. If you place an object 30 cm in front of the mirror, you can use the mirror formula to find the image distance. Plugging in the values, you can determine where the image will form and whether it will be real or virtual.

6. Applications of Spherical Mirrors

Spherical mirrors have numerous practical applications across various fields:

Optical Instruments: Concave mirrors are used in telescopes, microscopes, and cameras to focus light and form clear images. They help gather and direct light to enhance visibility.
Cosmetic Mirrors: Concave mirrors are commonly used in makeup and shaving mirrors, allowing users to see a magnified and upright image of their face.
Vehicle Mirrors: Convex mirrors are used as side mirrors in vehicles to provide a wider field of view, helping drivers see more of the area behind and beside them.
Security Mirrors: Convex mirrors are also used in stores and parking lots to monitor large areas, providing a broader perspective for security purposes.
Solar Cookers: Concave mirrors are used in solar cookers to concentrate sunlight onto a small area, generating heat for cooking.

Illustrative Explanation: Think of a makeup mirror that is slightly curved inward (concave). When you look into it, your reflection appears larger and clearer because the mirror focuses the light onto your face. In contrast, a convex mirror, like those used on the sides of cars, allows drivers to see a wider area behind them, although objects appear smaller.

Conclusion

Spherical mirrors are essential components in optics, providing valuable insights into the behavior of light and image formation. By exploring the definitions, types, characteristics, formation of images, mathematical formulations, examples, and applications of spherical mirrors, we gain a deeper appreciation for their significance in both natural and technological contexts. From the magnified reflections in a cosmetic mirror to the wide-angle views in vehicle side mirrors, spherical mirrors serve as powerful tools for enhancing our understanding of light and vision. As we continue to study and apply these principles, we unlock new possibilities for innovation and understanding in the world around us.

Blog.Pengayaan.Com