Electron spin is a fundamental property of electrons that plays a crucial role in quantum mechanics and atomic theory. It is a form of intrinsic angular momentum that is not associated with any physical spinning motion but is instead a quantum mechanical phenomenon. Understanding electron spin is essential for grasping the behavior of electrons in atoms, the nature of chemical bonds, and the principles underlying magnetism and quantum computing. This article aims to provide an exhaustive overview of electron spin, including its definition, mathematical representation, implications, and illustrative explanations of each concept to enhance understanding.
Definition of Electron Spin
1. Basic Definition:
- Electron spin is a quantum property of electrons that describes their intrinsic angular momentum. It is characterized by two possible states: “spin-up” (
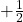) and “spin-down” (
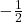). These states are often represented using arrows, where an upward arrow indicates spin-up and a downward arrow indicates spin-down.
Illustrative Explanation: Imagine a spinning top (electron) that can only spin in two distinct directions: clockwise (spin-up) and counterclockwise (spin-down). While the top does not physically spin in the classical sense, its orientation represents the two possible states of electron spin.
2. Quantum Mechanical Nature:
- Unlike classical angular momentum, which is associated with the motion of an object, electron spin is an intrinsic property that does not depend on any external factors. It is a fundamental characteristic of electrons and other fermions (particles with half-integer spin).
Illustrative Example: Think of a unique coin (electron) that has a built-in mechanism allowing it to show either heads (spin-up) or tails (spin-down) without ever physically flipping. This coin’s state is fixed and intrinsic, similar to how electron spin is a fundamental property of the particle.
Mathematical Representation of Electron Spin
1. Spin Quantum Number:
- The spin of an electron is described by a quantum number
, which for electrons is 
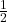. The possible values of the magnetic quantum number 
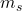associated with this spin are 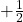and .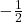
Illustrative Explanation: Imagine a scoreboard (quantum number) that tracks the performance of players (electrons). Each player can score either a positive point (spin-up) or a negative point (spin-down), but the maximum score (spin quantum number) for each player is fixed at half a point.
2. Pauli Exclusion Principle:
- The Pauli Exclusion Principle states that no two electrons in an atom can have the same set of quantum numbers. This principle is directly related to electron spin, as it ensures that each electron in an atom occupies a unique state.
Illustrative Example: Picture a classroom (atom) where each student (electron) has a unique ID number (quantum numbers). No two students can have the same ID, meaning that if one student is sitting in a specific seat (orbital) with a certain orientation (spin), another student cannot occupy that same seat with the same orientation.
3. Spinors:
- In quantum mechanics, the state of an electron’s spin can be represented using mathematical objects called spinors. A spinor is a complex vector that encodes the information about the spin state of a particle.
Illustrative Explanation: Think of a musical score (spinor) that contains the notes (spin states) for a specific piece of music (electron). Each note represents a different aspect of the music, and together they create a complete picture of the performance (spin state).
Implications of Electron Spin
1. Magnetism:
- Electron spin is a key factor in the magnetic properties of materials. Electrons with unpaired spins contribute to the overall magnetic moment of an atom, leading to phenomena such as paramagnetism and ferromagnetism.
Illustrative Explanation: Imagine a group of dancers (electrons) on a stage (atom) who can either dance in sync (paired spins) or independently (unpaired spins). When more dancers choose to dance independently, the overall performance (magnetic moment) becomes more dynamic and noticeable, similar to how unpaired electron spins contribute to magnetism.
2. Chemical Bonding:
- The concept of electron spin is crucial in understanding chemical bonding. In covalent bonds, electrons are shared between atoms, and their spins must be paired (one spin-up and one spin-down) to form a stable bond.
Illustrative Example: Picture two friends (atoms) holding hands (covalent bond) while spinning in opposite directions (paired spins). Their coordinated movement (paired spins) allows them to maintain their connection, while uncoordinated spinning would lead to a loss of balance (unstable bond).
3. Quantum Computing:
- Electron spin is a fundamental aspect of quantum computing, where the spin states of electrons can be used to represent quantum bits (qubits). Qubits can exist in superpositions of spin states, enabling quantum computers to perform complex calculations more efficiently than classical computers.
Illustrative Explanation: Imagine a library (quantum computer) where each book (qubit) can be open (spin-up) or closed (spin-down) at the same time. This unique ability allows the library to store and process vast amounts of information simultaneously, making it much more powerful than a traditional library that can only handle one book at a time.
Applications of Electron Spin
1. Spintronics:
- Spintronics is a field of technology that exploits the intrinsic spin of electrons, in addition to their charge, to develop new types of electronic devices. This technology has the potential to create faster and more efficient data storage and processing systems.
Illustrative Explanation: Think of a new type of bicycle (spintronic device) that uses both the pedals (charge) and the handlebars (spin) to enhance performance. By utilizing both components, the bicycle can travel faster and more efficiently than traditional bicycles that rely solely on pedals.
2. Magnetic Resonance Imaging (MRI):
- Electron spin is fundamental to the principles of magnetic resonance imaging (MRI), a medical imaging technique that uses the magnetic properties of atomic nuclei to create detailed images of the body. The alignment of spins in a magnetic field allows for the visualization of internal structures.
Illustrative Example: Imagine a photographer (MRI technician) using a special camera (MRI machine) that captures images based on the alignment of dancers (spins) in a formation (magnetic field). The resulting photographs provide a clear view of the performance (internal structures) from different angles.
3. Quantum Information Science:
- The study of electron spin is essential in quantum information science, where researchers explore the potential of using spin states for quantum communication and cryptography. The unique properties of electron spin can enhance the security and efficiency of information transfer.
Illustrative Explanation: Picture a secret messenger (quantum information) who can send messages (spin states) that can only be understood by the intended recipient (secure communication). The messenger’s ability to change the message based on their spin state ensures that only those with the right key can decode the information.
Conclusion
Electron spin is a fundamental property that provides critical insights into the behavior of electrons and their interactions in various physical and chemical processes. By exploring its definition, mathematical representation, implications, and applications, we gain valuable insights into the dynamics of atomic and subatomic systems. Just as a skilled conductor leads an orchestra to create a harmonious performance, the principles of electron spin orchestrate the interactions between particles, allowing us to predict and control their behavior. By mastering these concepts, we equip ourselves with the knowledge to analyze, predict, and influence the behavior of matter, enhancing our understanding of quantum mechanics, chemistry, and technology. Whether in the realms of magnetism, chemical bonding, or quantum computing, the principles surrounding electron spin are integral to the functioning of our world and our daily experiences