Hooke’s Law – Blog.Pengayaan.Com

Hooke’s Law is a fundamental principle in physics and engineering that describes the behavior of elastic materials when they are subjected to external forces. Named after the 17th-century British scientist Robert Hooke, this law provides a mathematical relationship between the force applied to a spring (or any elastic material) and the resulting deformation (displacement) of that material. This comprehensive overview will explore the definition of Hooke’s Law, its mathematical formulation, applications, limitations, and significance in various fields.

1. Definition of Hooke’s Law

Hooke’s Law states that the force exerted by a spring (or any elastic material) is directly proportional to the displacement or deformation of the spring from its equilibrium position, provided that the deformation is within the elastic limit of the material. In simpler terms, the more you stretch or compress a spring, the more force it exerts in the opposite direction.

2. Mathematical Formulation of Hooke’s Law

The mathematical expression of Hooke’s Law can be represented as:

$F = -k \cdot x$

Where:

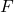$F$ = force exerted by the spring (in newtons, N)
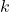$k$ = spring constant (in newtons per meter, N/m), which measures the stiffness of the spring
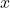$x$ = displacement from the equilibrium position (in meters, m)
The negative sign indicates that the force exerted by the spring is in the opposite direction to the displacement.

3. Understanding the Components of Hooke’s Law

A. Spring Constant ( $k$ ):
The spring constant is a measure of the stiffness of the spring. A higher value of $k$ indicates a stiffer spring that requires more force to produce a given displacement. Conversely, a lower value of $k$ indicates a more flexible spring. The spring constant can be determined experimentally by measuring the force required to stretch or compress the spring by a known amount.

B. Displacement ( $x$ ):
Displacement refers to the distance the spring is stretched or compressed from its natural (unstressed) length. Positive displacement indicates stretching, while negative displacement indicates compression.

4. Applications of Hooke’s Law

Hooke’s Law has numerous applications across various fields, including:

A. Mechanical Engineering:
In mechanical systems, Hooke’s Law is used to analyze the behavior of springs in suspension systems, shock absorbers, and various machinery components. Engineers use this law to design systems that can absorb energy and provide stability.

B. Civil Engineering:
In civil engineering, Hooke’s Law is applied to understand the behavior of materials under load, such as beams and columns. It helps engineers predict how structures will deform under various forces, ensuring safety and stability.

C. Material Science:
Hooke’s Law is fundamental in material science for studying the elastic properties of materials. It helps in characterizing materials and understanding their behavior under stress and strain.

D. Physics Education:
Hooke’s Law is often one of the first concepts introduced in physics education to illustrate the principles of elasticity and force. It provides a clear example of linear relationships in physics.

5. Limitations of Hooke’s Law

While Hooke’s Law is widely applicable, it has limitations:

A. Elastic Limit:
Hooke’s Law is only valid within the elastic limit of a material. If the applied force exceeds this limit, the material may undergo plastic deformation, meaning it will not return to its original shape after the force is removed. In such cases, Hooke’s Law no longer applies.

B. Non-Linear Behavior:
For some materials, especially those that are highly elastic or have complex structures, the relationship between force and displacement may not be linear. In these cases, more advanced models are required to describe their behavior accurately.

C. Temperature Dependence:
The spring constant $k$ can change with temperature. As materials heat up or cool down, their elastic properties may change, affecting the applicability of Hooke’s Law.

6. Graphical Representation of Hooke’s Law

The relationship described by Hooke’s Law can be graphically represented with a force-displacement graph. In this graph:

The x-axis represents the displacement ( $x$ ).
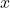The y-axis represents the force ( $F$ ).

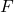The graph will show a straight line passing through the origin, indicating a linear relationship between force and displacement. The slope of this line corresponds to the spring constant $k$ .

Positive Slope: Indicates that the spring is being stretched (positive displacement).
Negative Slope: Indicates that the spring is being compressed (negative displacement).

7. Significance of Hooke’s Law

Hooke’s Law is significant for several reasons:

A. Fundamental Principle of Elasticity:
It serves as a foundational principle in the study of elasticity, providing insights into how materials respond to external forces.

B. Engineering Design:
Understanding Hooke’s Law allows engineers to design systems that effectively utilize springs and other elastic materials, ensuring safety and functionality.

C. Predictive Modeling:
Hooke’s Law enables predictive modeling of material behavior under various loads, which is essential for ensuring the integrity of structures and mechanical systems.

D. Interdisciplinary Applications:
The principles of Hooke’s Law extend beyond mechanical systems to fields such as biology (e.g., understanding the elasticity of biological tissues) and economics (e.g., modeling supply and demand relationships).

8. Conclusion

In conclusion, Hooke’s Law is a fundamental concept in physics and engineering that describes the relationship between the force exerted by a spring and its displacement from the equilibrium position. Its mathematical formulation, applications, limitations, and significance highlight its importance in various fields. While Hooke’s Law provides valuable insights into the behavior of elastic materials, it is essential to recognize its limitations and the conditions under which it applies. Understanding Hooke’s Law is crucial for engineers, scientists, and students, as it forms the basis for analyzing elastic behavior and designing systems that rely on the principles of elasticity.

Blog.Pengayaan.Com