Planck’s constant is a fundamental physical constant that plays a crucial role in quantum mechanics, linking the energy of a photon to its frequency. Named after the German physicist Max Planck, who introduced it in 1900, this constant is essential for understanding the behavior of particles at the quantum level. This article will delve into the definition of Planck’s constant, its mathematical representation, significance in quantum mechanics, applications, and illustrative explanations for each concept.
Definition of Planck’s Constant
Planck’s constant (
) is defined as the proportionality factor that relates the energy (
) of a photon to its frequency (
). The relationship is expressed by the equation:
![\[ E = h \nu \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-1836eb49e4c0128439de1e136ed175e8_l3.png "Rendered by QuickLaTeX.com")
Where:
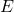- is the energy of the photon (measured in joules, J).
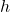- is Planck’s constant (approximately
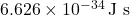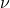). - is the frequency of the photon (measured in hertz, Hz).
Illustrative Explanation
To visualize this relationship, imagine a wave in the ocean. The frequency of the wave corresponds to how many wave crests pass a given point in one second. In the context of light, each photon can be thought of as a wave, and its energy is directly related to how fast those wave crests are moving (its frequency). Planck’s constant acts as a bridge that connects the wave-like properties of light to its particle-like properties, quantifying how much energy each photon carries based on its frequency.
Mathematical Representation of Planck’s Constant
Planck’s constant is a fundamental constant in physics, and its value is approximately:
![\[ h \approx 6.626 \times 10^{-34} \, \text{J s} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-d0e5813aa92d9a0ef54b49b8bc63a984_l3.png "Rendered by QuickLaTeX.com")
In some contexts, particularly in quantum mechanics, a reduced form of Planck’s constant, known as the reduced Planck’s constant (
), is used:
![\[ \hbar = \frac{h}{2\pi} \approx 1.055 \times 10^{-34} \, \text{J s} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-3dfac5e14639c6c9ec677e41dfedc24f_l3.png "Rendered by QuickLaTeX.com")
Illustrative Explanation
Think of Planck’s constant as a tiny ruler that measures the energy of photons. Just as a ruler can measure lengths in centimeters or inches, Planck’s constant provides a scale for quantifying the energy associated with the frequency of light. The reduced Planck’s constant () is often used in calculations involving angular momentum and wave functions, simplifying equations in quantum mechanics.
Significance of Planck’s Constant in Quantum Mechanics
Planck’s constant is significant for several reasons:
1. Quantum Theory Foundation: Planck’s constant is a cornerstone of quantum mechanics, marking the transition from classical physics to quantum physics. It introduced the concept of quantization, where energy levels are discrete rather than continuous.
Illustrative Explanation
Imagine a staircase versus a ramp. In classical physics, energy levels are like a ramp, allowing for any value of energy. In quantum mechanics, energy levels are like a staircase, where you can only step on specific levels (quantized energy states). Planck’s constant defines the height of each step, determining how much energy is required to move from one level to another.
2. Photoelectric Effect: The photoelectric effect, which was explained by Albert Einstein in 1905, demonstrates the particle-like behavior of light. When light shines on a metal surface, it can eject electrons if the energy of the photons exceeds a certain threshold. This phenomenon is directly related to Planck’s constant.
Illustrative Explanation
Picture a game where you need to hit a target with a ball. If the ball (photon) doesn’t have enough energy (frequency), it won’t knock the target (electron) down. Planck’s constant helps determine the minimum energy required for the ball to succeed. If the frequency of the light is too low, no electrons will be ejected, regardless of the intensity of the light.
3. Energy Quantization: Planck’s constant leads to the concept of quantized energy levels in atoms. Electrons can only occupy specific energy levels, and transitions between these levels involve the absorption or emission of photons with energy equal to the difference between the levels.
Illustrative Explanation
Imagine a ladder where each rung represents a specific energy level for an electron in an atom. An electron can only stand on these rungs and must jump from one to another by absorbing or emitting a photon. The energy of the photon corresponds to the height difference between the rungs, and Planck’s constant helps calculate this energy.
Applications of Planck’s Constant
Planck’s constant has numerous applications across various fields:
1. Quantum Mechanics: In quantum mechanics, Planck’s constant is used to describe the behavior of particles at the atomic and subatomic levels. It is essential for calculations involving wave functions, uncertainty principles, and energy quantization.
Illustrative Explanation
When physicists solve the Schrödinger equation to determine the behavior of an electron in an atom, they use Planck’s constant to account for the wave-like nature of the electron. This allows them to predict the probability of finding the electron in a particular region around the nucleus.
2. Spectroscopy: In spectroscopy, Planck’s constant is used to analyze the interaction of light with matter. It helps determine the energy levels of electrons in atoms and molecules, providing insights into their structure and behavior.
Illustrative Explanation
When scientists study the light emitted or absorbed by a substance, they can use Planck’s constant to calculate the energy of the photons involved. This information helps them identify the specific energy levels of electrons in the substance, revealing details about its chemical composition.
3. Quantum Computing: Planck’s constant is relevant in the field of quantum computing, where it helps define the behavior of qubits and the principles of superposition and entanglement.
Illustrative Explanation
In quantum computing, qubits can exist in multiple states simultaneously, similar to how a photon can have different frequencies. Planck’s constant helps quantify the energy associated with these states, allowing engineers to design quantum algorithms and circuits.
Conclusion
In conclusion, Planck’s constant is a fundamental physical constant that plays a crucial role in quantum mechanics, linking the energy of photons to their frequency. Understanding the definition, mathematical representation, significance in quantum mechanics, applications, and illustrative explanations of Planck’s constant is essential for grasping various physical phenomena. From the foundation of quantum theory to applications in spectroscopy and quantum computing, Planck’s constant is a vital component of our understanding of the microscopic world. By appreciating the intricacies of Planck’s constant, we can better navigate its implications in both scientific and practical contexts.