The Rhombus: A Comprehensive Exploration

A rhombus is a fascinating and unique geometric shape that belongs to the family of quadrilaterals. It is characterized by its equal-length sides and specific properties that distinguish it from other quadrilaterals, such as rectangles and squares. The study of the rhombus is essential in geometry, as it provides insights into the properties of shapes, symmetry, and area calculations. This article aims to provide an exhaustive overview of the rhombus, including its definition, properties, formulas, types, applications, and illustrative explanations for each concept.

1. Definition of a Rhombus

1.1. What is a Rhombus?

A rhombus is defined as a quadrilateral (a polygon with four sides) in which all four sides are of equal length. It can be thought of as a “tilted” square, where the angles are not necessarily $90^\circ$ . The opposite angles of a rhombus are equal, and the diagonals bisect each other at right angles.

Illustrative Explanation: Imagine a square that has been pushed over to one side. If you maintain the same side lengths but change the angles, you create a rhombus. For example, if each side of the rhombus measures $5$ units, then all four sides are equal, but the angles can vary.

1.2. Notation and Terminology

Vertices: The corners of the rhombus are called vertices. A rhombus has four vertices, typically labeled 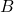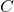$A$ , $B$ , $C$ , and $D$ .
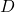Sides: The four equal-length edges of the rhombus.
Diagonals: The line segments that connect opposite vertices. In a rhombus, the diagonals bisect each other at right angles.

2. Properties of a Rhombus

2.1. Equal Sides

One of the defining properties of a rhombus is that all four sides are of equal length. This property is fundamental to the definition of a rhombus.

Illustrative Explanation: If you measure each side of a rhombus and find that they all measure $6$ units, you can confidently say that it is a rhombus.

2.2. Opposite Angles are Equal

In a rhombus, the opposite angles are equal. If one angle measures $60^\circ$ , the angle directly across from it will also measure $60^\circ$ , while the other two angles will each measure $120^\circ$ .

Illustrative Explanation: If you have a rhombus with angles $A$ , $B$ , $C$ , and $D$ , then:

$\angle A = \angle C \quad \text{and} \quad \angle B = \angle D$

2.3. Diagonals Bisect Each Other

The diagonals of a rhombus bisect each other at right angles. This means that each diagonal divides the other into two equal parts, and they intersect at $90^\circ$ .

Illustrative Explanation: If diagonal $AC$ intersects diagonal $BD$ at point $O$ , then:

$AO = OC \quad \text{and} \quad BO = OD$

Additionally, $\angle AOB = 90^\circ$ .

2.4. Diagonals are Perpendicular

The diagonals of a rhombus are not only bisected but are also perpendicular to each other. This property is unique to rhombuses and distinguishes them from other quadrilaterals.

Illustrative Explanation: If you draw the diagonals of a rhombus, you will see that they intersect at right angles, forming four right triangles within the rhombus.

2.5. Area of a Rhombus

The area $A$ of a rhombus can be calculated using the lengths of its diagonals $d_1$ and $d_2$ with the formula:

$A = \frac{1}{2} \times d_1 \times d_2$

Illustrative Explanation: If a rhombus has diagonals measuring $8$ units and $6$ units, the area would be:

$A = \frac{1}{2} \times 8 \times 6 = 24 \text{ square units}$

3. Types of Rhombuses

3.1. Regular Rhombus

A regular rhombus is a special case where all angles are equal, making it a square. In this case, each angle measures $90^\circ$ , and all sides are equal.

Illustrative Explanation: A square is a specific type of rhombus where not only are the sides equal, but the angles are also right angles.

3.2. Irregular Rhombus

An irregular rhombus has unequal angles but maintains equal side lengths. The angles can vary, but the property of equal sides remains.

Illustrative Explanation: An irregular rhombus might have angles of $70^\circ$ and $110^\circ$ , but all four sides will still be of equal length.

4. Applications of Rhombuses

4.1. Architecture and Design

Rhombuses are often used in architectural designs and patterns due to their aesthetic appeal and structural properties. They can be found in tiling patterns, window designs, and decorative elements.

Illustrative Explanation: A tiled floor may feature a rhombus pattern, creating a visually interesting design that enhances the overall appearance of the space.

4.2. Mathematics and Geometry

In mathematics, rhombuses are studied for their properties and relationships with other geometric shapes. They serve as examples in proofs and theorems related to quadrilaterals.

Illustrative Explanation: In geometry classes, students may be asked to prove that the diagonals of a rhombus bisect each other at right angles, reinforcing their understanding of geometric properties.

4.3. Art and Craft

Rhombuses are commonly used in art and craft projects, such as quilting, origami, and graphic design. Their unique shape allows for creative patterns and designs.

Illustrative Explanation: In quilting, a pattern may consist of multiple rhombus shapes arranged in a way that creates a visually appealing design.

5. Limitations of Rhombuses

5.1. Not All Quadrilaterals are Rhombuses

While all rhombuses are quadrilaterals, not all quadrilaterals are rhombuses. Quadrilaterals can have varying side lengths and angles, which may not satisfy the conditions of a rhombus.

5.2. Complexity in Real-World Applications

In real-world applications, the properties of rhombuses may not always be easily observable. For example, in engineering, the ideal conditions of a rhombus may be difficult to achieve due to material constraints.

5.3. Misinterpretation of Properties

Students may sometimes confuse the properties of rhombuses with those of other quadrilaterals, such as rectangles or squares. It is essential to understand the unique characteristics that define a rhombus.

Conclusion

In conclusion, the rhombus is a unique and important geometric shape characterized by its equal-length sides and specific properties. Understanding the definition, properties, types, and applications of rhombuses is essential for students and enthusiasts of geometry. The rhombus serves as a fundamental example in the study of quadrilaterals, providing insights into symmetry, area calculations, and geometric relationships. Whether in architecture, mathematics, or art, the rhombus continues to inspire creativity and curiosity, making it a vital topic in the exploration of geometric shapes. As we delve deeper into the world of geometry, the study of the rhombus will remain an essential part of our understanding of the relationships between shapes and their properties.

Blog.Pengayaan.Com