Kinematics is a branch of classical mechanics that deals with the motion of objects without considering the forces that cause this motion. It focuses on the description of motion in terms of displacement, velocity, acceleration, and time. Understanding kinematics is essential for analyzing the movement of objects in various fields, including physics, engineering, and robotics. This article will delve into the definition of kinematics, its fundamental concepts, equations of motion, types of motion, and applications, providing illustrative explanations for each concept.
Definition of Kinematics
Kinematics is defined as the study of the geometric aspects of motion. It describes how objects move in space and time, focusing on parameters such as position, velocity, and acceleration. Kinematics does not involve the forces that cause motion; instead, it provides a framework for understanding how objects change their position over time.
Illustrative Explanation
Imagine watching a car drive down a straight road. Kinematics allows you to describe the car’s journey by noting its starting position, how fast it is going (velocity), how that speed changes (acceleration), and how long it takes to reach its destination. You can analyze the car’s motion without needing to know why it is moving—whether it’s due to the engine’s power, friction, or any other forces.
Fundamental Concepts of Kinematics
Kinematics is built upon several fundamental concepts:
1. Displacement: Displacement is a vector quantity that represents the change in position of an object. It is defined as the difference between the final position and the initial position of the object. Displacement has both magnitude and direction.
Illustrative Explanation
Consider a person walking from point A to point B. If point A is at coordinates (2, 3) and point B is at (5, 7), the displacement can be calculated as:
![\[ \text{Displacement} = \text{Final Position} - \text{Initial Position} = (5, 7) - (2, 3) = (3, 4) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-a0304e19fcca3da62b73977a5c21d985_l3.png "Rendered by QuickLaTeX.com")
This means the person has moved 3 units in the x-direction and 4 units in the y-direction.
2. Distance: Distance is a scalar quantity that represents the total length of the path traveled by an object, regardless of direction. It is always positive and does not account for the direction of motion.
Illustrative Explanation
If the same person walks from point A to point B and then back to point A, the distance traveled is the total length of the path taken. If the distance from A to B is 5 units, the total distance for the round trip is:
![\[ \text{Total Distance} = 5 \, \text{units} + 5 \, \text{units} = 10 \, \text{units} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-cb5f663def76acaeaf97b251810a5495_l3.png "Rendered by QuickLaTeX.com")
3. Velocity: Velocity is a vector quantity that describes the rate of change of displacement with respect to time. It indicates both the speed and direction of an object’s motion. The average velocity (
) can be calculated using the formula:
![\[ v = \frac{\Delta x}{\Delta t} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-0cf6d44e10b092e7dd562fa95c9d7c1e_l3.png "Rendered by QuickLaTeX.com")
Where 
is the displacement and 
is the time interval.
Illustrative Explanation
If the person from the previous example takes 2 seconds to walk from point A to point B, the average velocity can be calculated as:
![\[ v = \frac{(5 - 2)}{2} = \frac{3}{2} = 1.5 \, \text{units/second} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-31dafad9ad41509852600a911cc3afc2_l3.png "Rendered by QuickLaTeX.com")
This means the person is moving at an average speed of 1.5 units per second in the direction from A to B.
4. Speed: Speed is a scalar quantity that represents the rate of change of distance with respect to time. It is the absolute value of velocity and does not include direction. The average speed (
) can be calculated using the formula:
![\[ s = \frac{\text{Total Distance}}{\Delta t} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-fbf2963eaaea9ccf2208e4049a7cbc54_l3.png "Rendered by QuickLaTeX.com")
Illustrative Explanation
Continuing with the previous example, if the person walked a total distance of 10 units in 4 seconds, the average speed would be:
![\[ s = \frac{10 \, \text{units}}{4 \, \text{seconds}} = 2.5 \, \text{units/second} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-696ea5547b146570daeb484ed8e09bc4_l3.png "Rendered by QuickLaTeX.com")
This indicates how fast the person is moving, regardless of direction.
5. Acceleration: Acceleration is a vector quantity that describes the rate of change of velocity with respect to time. It indicates how quickly an object is speeding up or slowing down. The average acceleration (
) can be calculated using the formula:
![\[ a = \frac{\Delta v}{\Delta t} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-73c5bd4d18b59179d791f62231fe524f_l3.png "Rendered by QuickLaTeX.com")
Where 
is the change in velocity.
Illustrative Explanation
If the person starts walking at a velocity of 1 m/s and increases to 3 m/s over 2 seconds, the average acceleration can be calculated as:
![\[ a = \frac{(3 - 1)}{2} = \frac{2}{2} = 1 \, \text{m/s}^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-0f25c1b2c856637884afe78b8dc574e1_l3.png "Rendered by QuickLaTeX.com")
This means the person is accelerating at a rate of 1 meter per second squared.
Equations of Motion
Kinematics is governed by a set of equations known as the equations of motion, which describe the relationship between displacement, velocity, acceleration, and time. These equations are particularly useful for uniformly accelerated motion (constant acceleration). The three primary equations of motion are:
1. First Equation of Motion:
![\[ v = u + at \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-a4bbe9a22197edd7a53649794e57731a_l3.png "Rendered by QuickLaTeX.com")
Where:
- is the final velocity.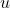
is the initial velocity.- is the acceleration.
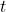is the time.
Illustrative Explanation
If a car starts from rest (initial velocity 
) and accelerates at 
for 
seconds, the final velocity can be calculated as:
![\[ v = 0 + (2)(5) = 10 \, \text{m/s} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-8e6953f3ded3ac614d4a206173088891_l3.png "Rendered by QuickLaTeX.com")
2. Second Equation of Motion:
![\[ s = ut + \frac{1}{2}at^2 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-956d5e2bc9705ff9ab425504deee779c_l3.png "Rendered by QuickLaTeX.com")
Where:
- is the displacement.
Illustrative Explanation
Using the same car example, if the car accelerates from rest for seconds, the displacement can be calculated as:
![\[ s = (0)(5) + \frac{1}{2}(2)(5^2) = 0 + \frac{1}{2}(2)(25) = 25 \, \text{m} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-7a2001b98e84ccf86e3d83b2b9b2e0d2_l3.png "Rendered by QuickLaTeX.com")
3. Third Equation of Motion:
![\[ v^2 = u^2 + 2as \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-1bc3e62b915210541fb0882da789d0c3_l3.png "Rendered by QuickLaTeX.com")
Where:
- is the displacement.
Illustrative Explanation
If the car accelerates at and travels 
, we can find the final velocity:
![\[ v^2 = 0^2 + 2(2)(25) = 0 + 100 \implies v = \sqrt{100} = 10 \, \text{m/s} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-a2cfa03a3306e6e19166dab7ce2165ff_l3.png "Rendered by QuickLaTeX.com")
Types of Motion
Kinematics can describe various types of motion, including:
1. Linear Motion: Motion along a straight line, characterized by constant velocity or acceleration. Examples include a car driving on a straight road or a ball rolling down a hill.
Illustrative Explanation
If a car travels in a straight line at a constant speed of 
, it exhibits linear motion. The distance covered over time can be calculated using the formula:
![\[ \text{Distance} = \text{Speed} \times \text{Time} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-06cfcbe1d73e13ce48bc3e27f39217f0_l3.png "Rendered by QuickLaTeX.com")
2. Projectile Motion: Motion of an object that is thrown or projected into the air, subject to gravitational acceleration. The path followed is a parabola.
Illustrative Explanation
When a basketball is thrown towards a hoop, it follows a curved trajectory. The horizontal and vertical motions can be analyzed separately, with the vertical motion affected by gravity.
3. Circular Motion: Motion of an object moving along a circular path. It can be uniform (constant speed) or non-uniform (changing speed).
Illustrative Explanation
A car driving around a circular track experiences circular motion. The speed may remain constant, but the direction of the car’s velocity changes continuously, requiring a centripetal force to keep it on the path.
Applications of Kinematics
Kinematics has numerous applications across various fields:
1. Engineering: Kinematics is essential in designing machines, vehicles, and structures. Engineers use kinematic principles to analyze motion and ensure safety and efficiency.
Illustrative Explanation
In automotive engineering, kinematics is used to design suspension systems that absorb shocks and maintain vehicle stability during motion.
2. Robotics: Kinematics is crucial in robotics for controlling the movement of robotic arms and autonomous vehicles. Understanding the motion of joints and links allows for precise control.
Illustrative Explanation
A robotic arm used in manufacturing must move accurately to pick up and place objects. Kinematic equations help programmers determine the necessary movements to achieve the desired position.
3. Sports Science: Kinematics is applied in sports science to analyze athletes’ movements, improve performance, and reduce the risk of injury.
Illustrative Explanation
Coaches may use kinematic analysis to study a sprinter’s running technique, identifying areas for improvement in stride length and frequency to enhance speed.
Conclusion
In conclusion, kinematics is a fundamental branch of classical mechanics that focuses on the motion of objects without considering the forces involved. Understanding the definition, fundamental concepts, equations of motion, types of motion, and applications of kinematics is essential for analyzing and predicting the behavior of moving objects. From engineering to robotics and sports science, kinematics plays a vital role in various fields, providing insights into the dynamics of motion. By appreciating the intricacies of kinematics, we can better navigate its implications in both scientific and practical contexts.