Rational Numbers and Their Properties: A Comprehensive Overview

Rational numbers are a fundamental concept in mathematics, representing a class of numbers that can be expressed as the quotient of two integers. Understanding rational numbers and their properties is essential for various mathematical applications, including arithmetic, algebra, and number theory. This article will provide an exhaustive exploration of rational numbers, covering their definitions, characteristics, types, operations, and properties, along with illustrative explanations of each concept.

Definition of Rational Numbers

A rational number is defined as any number that can be expressed in the form of a fraction $\frac{p}{q}$ , where:

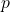$p$ is an integer (the numerator),
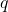$q$ is a non-zero integer (the denominator).

This definition implies that rational numbers can be positive, negative, or zero. For example, $\frac{3}{4}$ , $-\frac{5}{2}$ , and $0$ (which can be expressed as $\frac{0}{1}$ ) are all rational numbers.

Characteristics of Rational Numbers

1. Finite or Repeating Decimals: Rational numbers can be represented as either finite decimals or repeating decimals. A finite decimal has a limited number of digits after the decimal point, while a repeating decimal has a sequence of digits that repeats indefinitely.

– Illustrative Explanation:
– The rational number $\frac{1}{4}$ can be expressed as the finite decimal $0.25$ .
– The rational number $\frac{1}{3}$ can be expressed as the repeating decimal $0.333...$ (often written as $0.\overline{3}$ ).

2. Closure Property: The set of rational numbers is closed under addition, subtraction, multiplication, and division (except by zero). This means that performing these operations on rational numbers will always yield another rational number.

– Illustrative Explanation:
– If we take two rational numbers, $\frac{1}{2}$ and $\frac{3}{4}$ :
– Addition: $\frac{1}{2} + \frac{3}{4} = \frac{2}{4} + \frac{3}{4} = \frac{5}{4}$ (which is rational).
– Subtraction: $\frac{3}{4} - \frac{1}{2} = \frac{3}{4} - \frac{2}{4} = \frac{1}{4}$ (which is rational).
– Multiplication: $\frac{1}{2} \times \frac{3}{4} = \frac{3}{8}$ (which is rational).
– Division: $\frac{3}{4} \div \frac{1}{2} = \frac{3}{4} \times \frac{2}{1} = \frac{3 \times 2}{4 \times 1} = \frac{6}{4} = \frac{3}{2}$ (which is rational).

3. Density Property: Between any two rational numbers, there exists another rational number. This property indicates that rational numbers are dense on the number line.

– Illustrative Explanation:
– Consider the rational numbers $\frac{1}{2}$ and $\frac{3}{4}$ . A rational number that lies between them is $\frac{5}{8}$ :

$\frac{1}{2} = \frac{4}{8} \quad \text{and} \quad \frac{3}{4} = \frac{6}{8}$

– Thus, $\frac{4}{8} < \frac{5}{8} < \frac{6}{8}$ .

Types of Rational Numbers

Rational numbers can be categorized into several types based on their characteristics:

1. Positive Rational Numbers: These are rational numbers greater than zero. They can be expressed as fractions where both the numerator and denominator are positive integers.

– Illustrative Example: $\frac{3}{5}$ and $\frac{7}{2}$ are positive rational numbers.

2. Negative Rational Numbers: These are rational numbers less than zero. They can be expressed as fractions where either the numerator or the denominator is negative, but not both.

– Illustrative Example: $-\frac{4}{3}$ and $\frac{-5}{6}$ are negative rational numbers.

3. Zero: Zero is considered a rational number because it can be expressed as $\frac{0}{1}$ or $\frac{0}{n}$ for any non-zero integer $n$ .

4. Improper Fractions: These are fractions where the absolute value of the numerator is greater than or equal to the absolute value of the denominator. Improper fractions can be converted into mixed numbers.

– Illustrative Example: $\frac{9}{4}$ is an improper fraction, which can be expressed as $2 \frac{1}{4}$ .

5. Proper Fractions: These are fractions where the absolute value of the numerator is less than the absolute value of the denominator.

– Illustrative Example: $\frac{3}{8}$ is a proper fraction.

Operations with Rational Numbers

Rational numbers can be added, subtracted, multiplied, and divided using standard arithmetic rules. Here’s how each operation works:

1. Addition: To add two rational numbers, find a common denominator, add the numerators, and simplify if necessary.

– Illustrative Example:

$\frac{1}{3} + \frac{1}{6} = \frac{2}{6} + \frac{1}{6} = \frac{3}{6} = \frac{1}{2}$

2. Subtraction: Similar to addition, find a common denominator, subtract the numerators, and simplify.

– Illustrative Example:

$\frac{5}{6} - \frac{1}{3} = \frac{5}{6} - \frac{2}{6} = \frac{3}{6} = \frac{1}{2}$

3. Multiplication: Multiply the numerators together and the denominators together.

– Illustrative Example:

$\frac{2}{3} \times \frac{4}{5} = \frac{2 \times 4}{3 \times 5} = \frac{8}{15}$

4. Division: To divide by a rational number, multiply by its reciprocal.

– Illustrative Example:

$\frac{3}{4} \div \frac{2}{5} = \frac{3}{4} \times \frac{5}{2} = \frac{15}{8}$

Properties of Rational Numbers

1. Commutative Property: The order of addition and multiplication does not affect the result.

– Illustrative Explanation:
– For addition: $\frac{1}{2} + \frac{1}{3} = \frac{1}{3} + \frac{1}{2}$
– For multiplication: $\frac{2}{5} \times \frac{3}{4} = \frac{3}{4} \times \frac{2}{5}$

2. Associative Property: The grouping of numbers does not affect the result of addition and multiplication.

– Illustrative Explanation:
– For addition: $\left(\frac{1}{2} + \frac{1}{3}\right) + \frac{1}{4} = \frac{1}{2} + \left(\frac{1}{3} + \frac{1}{4}\right)$
– For multiplication: $\left(\frac{2}{5} \times \frac{3}{4}\right) \times \frac{1}{2} = \frac{2}{5} \times \left(\frac{3}{4} \times \frac{1}{2}\right)$

3. Distributive Property: Multiplication distributes over addition.

– Illustrative Explanation:
– $\frac{1}{2} \times \left(\frac{3}{4} + \frac{1}{4}\right) = \frac{1}{2} \times \frac{4}{4} = \frac{1}{2}$
– $\frac{1}{2} \times \frac{3}{4} + \frac{1}{2} \times \frac{1}{4} = \frac{3}{8} + \frac{1}{8} = \frac{4}{8} = \frac{1}{2}$

4. Identity Elements: The identity element for addition is $0$ (since $a + 0 = a$ ), and for multiplication, it is $1$ (since $a \times 1 = a$ ).

5. Inverse Elements: For every rational number $a$ , there exists an additive inverse $-a$ such that $a + (-a) = 0$ , and a multiplicative inverse $\frac{1}{a}$ (where $a \neq 0$ ) such that $a \times \frac{1}{a} = 1$ .

Conclusion

Rational numbers are a vital part of mathematics, encompassing a wide range of values that can be expressed as fractions. Their properties, including closure under operations, density on the number line, and the ability to represent both finite and repeating decimals, make them essential for various mathematical applications.

By understanding the characteristics, types, operations, and properties of rational numbers, students and professionals can enhance their mathematical skills and apply these concepts in real-world scenarios. Whether in arithmetic, algebra, or advanced mathematics, rational numbers play a crucial role in shaping our understanding of numerical relationships and calculations. As we continue to explore the world of numbers, rational numbers remain a foundational element that bridges the gap between integers and real numbers, enriching our mathematical journey.

Blog.Pengayaan.Com

Rational Numbers and Their Properties: A Comprehensive Overview

Definition of Rational Numbers

Characteristics of Rational Numbers

Types of Rational Numbers

Operations with Rational Numbers

Properties of Rational Numbers

Conclusion

Leave a Reply Cancel reply