Understanding Kirchhoff’s Second Law: A Comprehensive Overview

Kirchhoff’s Second Law, also known as the Voltage Law or Kirchhoff’s Loop Law, is a fundamental principle in electrical engineering and circuit analysis. It plays a crucial role in understanding how electrical circuits function by providing a method to analyze the voltages in a closed loop. This article will provide a detailed exploration of Kirchhoff’s Second Law, including its definition, mathematical formulation, applications, and illustrative explanations to enhance understanding.

1. Definition of Kirchhoff’s Second Law

Kirchhoff’s Second Law states that the sum of the electromotive forces (emf) and the potential differences (voltage drops) in any closed loop of an electrical circuit is equal to zero. In simpler terms, this means that the total voltage around any closed loop in a circuit must equal the total voltage drops across the components within that loop.

Mathematical Expression

The mathematical expression for Kirchhoff’s Second Law can be written as:

$\sum V = 0$

Where:

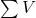$\sum V$ represents the sum of all voltages in the loop, including both the electromotive forces (sources of voltage) and the voltage drops across resistive elements.

Illustrative Explanation: Imagine a circular track where runners start and finish at the same point. If you measure the distance they cover in one complete lap, the total distance traveled (voltage) must equal zero when they return to the starting point. Similarly, in an electrical circuit, the total voltage supplied by sources must balance out with the voltage drops across the components in the loop.

2. Understanding Voltage Drops and EMF

A. Electromotive Force (EMF)

Electromotive force (emf) refers to the voltage generated by a source, such as a battery or generator, when no current is flowing. It represents the energy provided per unit charge by the source.

Illustrative Explanation: Think of a water pump that pushes water into a tank. The pump’s pressure (emf) represents the energy supplied to move the water. When the pump is running, it creates a potential difference that drives the flow of water (current) through the system.

B. Voltage Drops

Voltage drops occur across components in a circuit, such as resistors, capacitors, and inductors, due to the energy consumed by these components as current flows through them. The voltage drop across a resistor can be calculated using Ohm’s Law:

$V = IR$

Where:

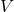$V$ is the voltage drop,
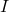$I$ is the current flowing through the resistor,
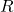$R$ is the resistance.

Illustrative Explanation: Imagine a series of water pipes with different diameters. As water flows through each pipe, some energy is lost due to friction (voltage drop). The larger the resistance (narrower the pipe), the more energy is lost, resulting in a greater voltage drop.

3. Application of Kirchhoff’s Second Law

Kirchhoff’s Second Law is widely used in circuit analysis to determine unknown voltages and currents in complex circuits. It is particularly useful in the following scenarios:

A. Analyzing Series Circuits

In a series circuit, components are connected end-to-end, and the same current flows through each component. Kirchhoff’s Second Law can be applied to find the voltage across each component.

Illustrative Explanation: Imagine a string of Christmas lights connected in a series. If one bulb goes out (like a resistor failing), the entire string goes dark. The total voltage from the power source is divided among the bulbs, and Kirchhoff’s Second Law helps determine how much voltage each bulb receives.

B. Analyzing Parallel Circuits

In parallel circuits, components are connected across the same voltage source, and the voltage across each component is the same. Kirchhoff’s Second Law can be used to analyze the voltage drops across each branch of the circuit.

Illustrative Explanation: Think of a multi-lane highway where each lane represents a different path for cars (current) to travel. Each lane has the same speed limit (voltage), and Kirchhoff’s Second Law helps ensure that the total flow of traffic (current) is balanced across all lanes.

C. Complex Circuit Analysis

In more complex circuits with multiple loops and branches, Kirchhoff’s Second Law can be combined with Kirchhoff’s First Law (the Current Law) to create a system of equations that can be solved to find unknown voltages and currents.

Illustrative Explanation: Imagine a city with multiple intersections and roads. To navigate the city (analyze the circuit), you need to know the rules of the road (Kirchhoff’s Laws) to determine the best route (current flow) and ensure you reach your destination (desired voltage).

4. Example of Kirchhoff’s Second Law in Action

A. Simple Circuit Example

Consider a simple circuit with a 12V battery and two resistors, $R_1 = 4 \, \Omega$ and $R_2 = 8 \, \Omega$ , connected in series.

1. Identify the Loop: The loop consists of the battery and the two resistors.
2. Apply Kirchhoff’s Second Law:
– The total voltage supplied by the battery is 12V.
– The voltage drop across $R_1$ can be calculated using Ohm’s Law:

$V_1 = I \cdot R_1$

– The voltage drop across $R_2$ is:

$V_2 = I \cdot R_2$

3. Set Up the Equation:

$12V - V_1 - V_2 = 0$

Substituting the voltage drops:

$12V - I \cdot 4\Omega - I \cdot 8\Omega = 0$

Simplifying gives:

$12V = I \cdot 12\Omega$

Thus, the current $I$ is:

$I = 1A$

Illustrative Explanation: In this example, the battery provides 12V, which is divided between the two resistors. Kirchhoff’s Second Law ensures that the total voltage supplied equals the total voltage dropped across the resistors, maintaining balance in the circuit.

5. Limitations of Kirchhoff’s Second Law

While Kirchhoff’s Second Law is a powerful tool for circuit analysis, it does have limitations:

A. High-Frequency Circuits

In high-frequency circuits, the assumptions of Kirchhoff’s Laws may not hold due to parasitic capacitance and inductance, which can affect voltage and current distribution.

Illustrative Explanation: Imagine a fast-moving train that creates a wake in the water. At high speeds, the water’s behavior changes, and the simple rules of motion may not apply. Similarly, in high-frequency circuits, additional factors must be considered.

B. Non-Ideal Components

Real-world components may not behave ideally, leading to discrepancies in voltage and current measurements. Factors such as temperature, aging, and manufacturing tolerances can affect circuit performance.

Illustrative Explanation: Think of a rubber band that stretches differently based on temperature. In the same way, real components may not always follow the ideal behavior predicted by Kirchhoff’s Laws.

6. Conclusion

In summary, Kirchhoff’s Second Law is a fundamental principle in electrical engineering that provides a method for analyzing voltages in closed loops of electrical circuits. By stating that the sum of the electromotive forces and potential differences in a loop is zero, it allows engineers and technicians to understand and design complex circuits effectively. Through illustrative explanations and practical applications, we can appreciate the significance of Kirchhoff’s Second Law in ensuring the proper functioning of electrical systems. As technology continues to advance, the principles of Kirchhoff’s Laws will remain essential tools in the analysis and design of electrical circuits, ensuring reliable and efficient operation in a wide range of applications.

Blog.Pengayaan.Com