L’Hôpital’s Rule is a powerful tool in calculus used to evaluate limits that result in indeterminate forms. Named after the French mathematician Guillaume de l’Hôpital, this rule provides a systematic way to resolve limits that would otherwise be difficult to compute. Understanding L’Hôpital’s Rule is essential for students and professionals dealing with calculus, particularly in the fields of mathematics, physics, and engineering. This article aims to provide an exhaustive overview of L’Hôpital’s Rule, detailing its definition, conditions for application, step-by-step procedures, and illustrative explanations for each concept.
1. Understanding Indeterminate Forms
Before delving into L’Hôpital’s Rule, it is crucial to understand what indeterminate forms are. An indeterminate form arises when evaluating a limit leads to an ambiguous result. The most common indeterminate forms are:
1. 0/0: This occurs when both the numerator and denominator approach zero.
2. ∞/∞: This occurs when both the numerator and denominator approach infinity.
3. 0 × ∞: This occurs when one factor approaches zero while the other approaches infinity.
4. ∞ – ∞: This occurs when two infinite quantities are subtracted.
5. 0^0: This occurs when a base approaching zero is raised to an exponent approaching zero.
6. 1^∞: This occurs when a base approaching one is raised to an infinite exponent.
7. ∞^0: This occurs when an infinite base is raised to a power approaching zero.
- Illustrative Explanation: Imagine trying to determine the height of a plant that is growing at a rate that varies unpredictably. If you measure its height at two different times and find that it is both 0 cm and ∞ cm, you face an indeterminate situation. This ambiguity is what L’Hôpital’s Rule helps to resolve.
2. L’Hôpital’s Rule: Definition and Conditions
L’Hôpital’s Rule states that if you have a limit of the form 
that results in an indeterminate form (specifically 
or 
), you can take the derivative of the numerator and the derivative of the denominator separately and then evaluate the limit again. Mathematically, it can be expressed as:
![\[ \text{If } \lim_{x \to c} f(x) = 0 \text{ and } \lim_{x \to c} g(x) = 0 \text{ or } \lim_{x \to c} f(x) = \pm \infty \text{ and } \lim_{x \to c} g(x) = \pm \infty, \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-75761513483c1ad4ebd159ee276aeb48_l3.png "Rendered by QuickLaTeX.com")
![\[ \text{then } \lim_{x \to c} \frac{f(x)}{g(x)} = \lim_{x \to c} \frac{f'(x)}{g'(x)} \text{ (if this limit exists).} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-9b04922ce9126e87c5e6b1c7188c1135_l3.png "Rendered by QuickLaTeX.com")
Conditions for Application
1. The limit must be in the form or .
2. The functions 
and 
must be differentiable in an open interval around 
(except possibly at itself).
3. The limit of the derivatives 
must exist or approach 
.
- Illustrative Explanation: Think of L’Hôpital’s Rule as a tool that allows you to “zoom in” on the behavior of a function near a point of interest. If you encounter a situation where the function’s behavior is unclear (like a foggy view), taking the derivative is like clearing the fog to see the underlying trend more clearly.
3. Step-by-Step Application of L’Hôpital’s Rule
To apply L’Hôpital’s Rule effectively, follow these steps:
Step 1: Identify the Indeterminate Form
Evaluate the limit 
. If it results in or , you can apply L’Hôpital’s Rule.
Step 2: Differentiate the Numerator and Denominator
Compute the derivatives 
and 
.
Step 3: Re-evaluate the Limit
Evaluate the new limit 
. If this limit still results in an indeterminate form, you can apply L’Hôpital’s Rule again.
Step 4: Conclude
If the limit exists after applying the rule, state the result. If it continues to yield an indeterminate form, you may need to apply the rule multiple times or consider alternative methods.
- Illustrative Explanation: Imagine you are trying to find the speed of a car at a specific moment, but your speedometer is stuck at 0. By taking the derivative of the distance over time, you can get a clearer picture of the car’s speed at that moment, just as L’Hôpital’s Rule helps clarify limits.
4. Examples of L’Hôpital’s Rule
Example 1: Basic Application
Evaluate the limit:
![\[ \lim_{x \to 0} \frac{\sin(x)}{x} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-f5c37dd02793690e8ff733d623707f81_l3.png "Rendered by QuickLaTeX.com")
Step 1: Substitute 
:
![\[ \frac{\sin(0)}{0} = \frac{0}{0} \text{ (indeterminate form)} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-7d4f0f0dd014fd02128f97c2944baee0_l3.png "Rendered by QuickLaTeX.com")
Step 2: Differentiate:
→ 
→ 
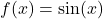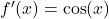
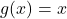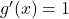
Step 3: Re-evaluate the limit:
![\[ \lim_{x \to 0} \frac{\cos(x)}{1} = \cos(0) = 1 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-7f358db7c058de0156eb8a81ce3c2b5b_l3.png "Rendered by QuickLaTeX.com")
Conclusion:
![\[ \lim_{x \to 0} \frac{\sin(x)}{x} = 1 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-ea9a60fd50a03549251e985373f530fd_l3.png "Rendered by QuickLaTeX.com")
Example 2: Applying L’Hôpital’s Rule Multiple Times
Evaluate the limit:
![\[ \lim_{x \to 0} \frac{e^x - 1}{x} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-b1412ac1af8334879b6ebe648b609d3a_l3.png "Rendered by QuickLaTeX.com")
Step 1: Substitute :
![\[ \frac{e^0 - 1}{0} = \frac{0}{0} \text{ (indeterminate form)} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-efd8d4faa0b77a066bdaaab57298f4bd_l3.png "Rendered by QuickLaTeX.com")
Step 2: Differentiate:
→ 
- →
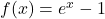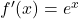
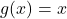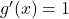
Step 3: Re-evaluate the limit:
![\[ \lim_{x \to 0} \frac{e^x}{1} = e^0 = 1 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-10a42c3e27768db7ae26a795f587e00f_l3.png "Rendered by QuickLaTeX.com")
Conclusion:
![\[ \lim_{x \to 0} \frac{e^x - 1}{x} = 1 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-9399b602977b7fc4cb9f3f3b845be80a_l3.png "Rendered by QuickLaTeX.com")
Example 3: Higher-Order Indeterminate Forms
Evaluate the limit:
![\[ \lim_{x \to 0} \frac{x^2}{\sin(x)} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-30032a17ef391662c57536c797b11883_l3.png "Rendered by QuickLaTeX.com")
Step 1: Substitute :
![\[ \frac{0^2}{\sin(0)} = \frac{0}{0} \text{ (indeterminate form)} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-cebb399e27d2d75f3bda912491e84eb3_l3.png "Rendered by QuickLaTeX.com")
Step 2: Differentiate:
→ 
→ 
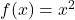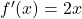
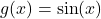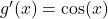
Step 3: Re-evaluate the limit:
![\[ \lim_{x \to 0} \frac{2x}{\cos(x)} = \frac{2 \cdot 0}{\cos(0)} = \frac{0}{1} = 0 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-745b87fb6d9cb9aefa11f6dc2162f57b_l3.png "Rendered by QuickLaTeX.com")
Conclusion:
![\[ \lim_{x \to 0} \frac{x^2}{\sin(x)} = 0 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-379b1267bc7955669c5adbc90f412ebd_l3.png "Rendered by QuickLaTeX.com")
5. Common Misconceptions and Pitfalls
1. Not All Limits Can Use L’Hôpital’s Rule: Remember that L’Hôpital’s Rule only applies to the specific indeterminate forms and . If the limit does not result in these forms, other techniques must be used.
2. Multiple Applications: Sometimes, applying L’Hôpital’s Rule once is not enough. If the new limit still results in an indeterminate form, you may need to apply the rule multiple times.
3. Existence of the Limit: Just because you can apply L’Hôpital’s Rule does not guarantee that the limit exists. Always check the final result after applying the rule.
- Illustrative Explanation: Think of L’Hôpital’s Rule as a tool in a toolbox. Just because you have the tool doesn’t mean it will fix every problem. You need to ensure it’s the right tool for the job.
Conclusion
In conclusion, L’Hôpital’s Rule is an essential technique in calculus for evaluating limits that result in indeterminate forms. By understanding the conditions for its application and following a systematic approach, you can effectively resolve complex limits. This rule not only simplifies the process of finding limits but also deepens your understanding of the behavior of functions near points of interest. As you continue your studies in calculus and beyond, mastering L’Hôpital’s Rule will serve as a valuable asset in your mathematical toolkit.