Trigonometry is a branch of mathematics that studies the relationships between the angles and sides of triangles, particularly right-angled triangles. The term “trigonometry” is derived from the Greek words “trigonon,” meaning triangle, and “metron,” meaning measure. This field of mathematics has applications in various disciplines, including physics, engineering, astronomy, and computer graphics. This article aims to provide an exhaustive overview of trigonometry, detailing its history, fundamental concepts, key functions, identities, applications, and illustrative explanations for each concept.
1. History of Trigonometry
1.1. Ancient Origins
The origins of trigonometry can be traced back to ancient civilizations, including the Egyptians and Babylonians, who used basic geometric principles to solve practical problems. However, the systematic study of trigonometry began with the Greeks, particularly with mathematicians such as Hipparchus and Ptolemy, who developed early trigonometric tables.
1.2. Development in the Middle Ages
During the Middle Ages, Islamic scholars made significant contributions to trigonometry. They translated Greek texts and expanded upon them, introducing new concepts and methods. Notable figures such as Al-Khwarizmi and Al-Battani developed trigonometric functions and tables that laid the groundwork for modern trigonometry.
1.3. Modern Trigonometry
The development of trigonometry continued into the Renaissance and beyond, with mathematicians like Johannes Kepler and Isaac Newton applying trigonometric principles to astronomy and calculus. Today, trigonometry is a fundamental part of mathematics education and is widely used in various scientific fields.
2. Fundamental Concepts of Trigonometry
2.1. Triangles and Angles
Trigonometry primarily deals with triangles, especially right-angled triangles. A right-angled triangle has one angle measuring ![]() . The other two angles are complementary, meaning they add up to
. The other two angles are complementary, meaning they add up to ![]() .
.
Illustrative Explanation: In a right-angled triangle ![]() , where
, where ![]() is the right angle, the sides are labeled as follows:
is the right angle, the sides are labeled as follows:
- Hypotenuse: The side opposite the right angle, denoted as
 .
. - Opposite Side: The side opposite the angle of interest, denoted as
 .
. - Adjacent Side: The side next to the angle of interest, denoted as
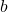 .
.
2.2. Trigonometric Ratios
The primary trigonometric ratios are defined based on the relationships between the sides of a right-angled triangle. These ratios are:
- Sine (sin): The ratio of the length of the opposite side to the length of the hypotenuse.
![]()
- Cosine (cos): The ratio of the length of the adjacent side to the length of the hypotenuse.
![]()
- Tangent (tan): The ratio of the length of the opposite side to the length of the adjacent side.
![]()
Illustrative Explanation: In triangle ![]() , if
, if ![]() is the angle of interest, then:
is the angle of interest, then:
- If
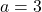 ,
, 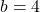 , and
, and 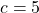 , then:
, then:
– ![]()
– ![]()
– ![]()
2.3. Reciprocal Trigonometric Ratios
In addition to the primary trigonometric ratios, there are reciprocal functions:
- Cosecant (csc): The reciprocal of sine.
![]()
- Secant (sec): The reciprocal of cosine.
![]()
- Cotangent (cot): The reciprocal of tangent.
![]()
Illustrative Explanation: Continuing with triangle ![]() :
:
- If
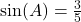 , then
, then 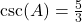 .
. - If
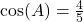 , then
, then 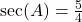 .
. - If
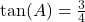 , then
, then 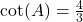 .
.
3. The Unit Circle
3.1. Definition of the Unit Circle
The unit circle is a circle with a radius of ![]() centered at the origin of a coordinate plane. It is a fundamental concept in trigonometry, as it provides a geometric interpretation of the trigonometric functions.
centered at the origin of a coordinate plane. It is a fundamental concept in trigonometry, as it provides a geometric interpretation of the trigonometric functions.
3.2. Coordinates on the Unit Circle
Any point on the unit circle can be represented as ![]() , where
, where ![]() is the angle formed with the positive x-axis. The x-coordinate corresponds to the cosine of the angle, while the y-coordinate corresponds to the sine of the angle.
is the angle formed with the positive x-axis. The x-coordinate corresponds to the cosine of the angle, while the y-coordinate corresponds to the sine of the angle.
Illustrative Explanation: For an angle of ![]() (or
(or ![]() radians), the coordinates on the unit circle are:
radians), the coordinates on the unit circle are:
![Rendered by QuickLaTeX.com \[ \left(\cos\left(30^\circ\right), \sin\left(30^\circ\right)\right) = \left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-ea0dc9ff1186517cda4a547012c0caaa_l3.png)
3.3. Trigonometric Functions on the Unit Circle
The unit circle allows for the definition of trigonometric functions for all angles, including those greater than ![]() and negative angles. The sine and cosine functions can be extended to all real numbers using the unit circle.
and negative angles. The sine and cosine functions can be extended to all real numbers using the unit circle.
Illustrative Explanation: For an angle of ![]() , which is in the third quadrant, the coordinates are:
, which is in the third quadrant, the coordinates are:
![Rendered by QuickLaTeX.com \[ \left(\cos\left(210^\circ\right), \sin\left(210^\circ\right)\right) = \left(-\frac{\sqrt{3}}{2}, -\frac{1}{2}\right) \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-03eca3a9429202f233e5670be2ea0bcd_l3.png)
4. Trigonometric Identities
Trigonometric identities are equations that hold true for all values of the variables involved. These identities are essential for simplifying expressions and solving trigonometric equations. Some key identities include:
4.1. Pythagorean Identities
The Pythagorean identities are derived from the Pythagorean theorem and relate the squares of the sine and cosine functions:
1. ![]()
2. ![]()
3. ![]()
Illustrative Explanation: If ![]() and
and ![]() , then:
, then:
![Rendered by QuickLaTeX.com \[ \left(\frac{1}{2}\right)^2 + \left(\frac{\sqrt{3}}{2}\right)^2 = \frac{1}{4} + \frac{3}{4} = 1 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-87bcb9429f25df5a75d550ef3611ecc8_l3.png)
4.2. Angle Sum and Difference Identities
These identities express the sine and cosine of the sum or difference of two angles:
- Sine:
– ![]()
– ![]()
- Cosine:
– ![]()
– ![]()
Illustrative Explanation: For ![]() and
and ![]() :
:
![]()
Substituting the values:
![Rendered by QuickLaTeX.com \[ \sin(75^\circ) = \left(\frac{1}{2}\right)\left(\frac{\sqrt{2}}{2}\right) + \left(\frac{\sqrt{3}}{2}\right)\left(\frac{\sqrt{2}}{2}\right) = \frac{\sqrt{2}}{4} + \frac{\sqrt{6}}{4} = \frac{\sqrt{2} + \sqrt{6}}{4} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-eacdb2404ae5fe267a95e3266d5fa6ec_l3.png)
4.3. Double Angle Identities
These identities express the sine and cosine of double angles:
Illustrative Explanation: For ![]() :
:
![Rendered by QuickLaTeX.com \[ \sin(60^\circ) = 2\sin(30^\circ)\cos(30^\circ) = 2\left(\frac{1}{2}\right)\left(\frac{\sqrt{3}}{2}\right) = \frac{\sqrt{3}}{2} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-55d9084a0b2a61011205272f6da57e5a_l3.png)
5. Applications of Trigonometry
5.1. Physics
Trigonometry is widely used in physics to analyze wave motion, oscillations, and forces. It helps in understanding concepts such as projectile motion and circular motion.
Illustrative Explanation: When analyzing the motion of a pendulum, trigonometric functions can describe the height and angle of the pendulum at any given time.
5.2. Engineering
In engineering, trigonometry is essential for designing structures, analyzing forces, and solving problems related to angles and distances.
Illustrative Explanation: Civil engineers use trigonometry to calculate the angles and lengths of beams and supports in buildings and bridges.
5.3. Astronomy
Astronomers use trigonometry to calculate distances to stars and planets, as well as to determine the positions of celestial bodies.
Illustrative Explanation: The parallax method, which involves measuring the apparent shift of a star’s position from different points in Earth’s orbit, relies on trigonometric calculations.
5.4. Computer Graphics
In computer graphics, trigonometry is used to create realistic animations and models by calculating angles, distances, and transformations.
Illustrative Explanation: When rendering a 3D object on a 2D screen, trigonometric functions help determine how the object should be displayed based on the viewer’s perspective.
6. Limitations of Trigonometry
6.1. Complexity of Functions
Trigonometric functions can be complex, especially when dealing with angles beyond the standard range. Understanding their periodic nature and transformations can be challenging for students.
6.2. Measurement Errors
In practical applications, measurement errors can lead to inaccuracies in calculations involving trigonometric functions. Small errors in angle measurement can result in significant discrepancies in distance calculations.
6.3. Dependence on Angles
Trigonometry is primarily concerned with angles and triangles, which may limit its applicability in certain mathematical contexts that do not involve these concepts.
Conclusion
In conclusion, trigonometry is a vital branch of mathematics that explores the relationships between angles and sides of triangles. Its historical development, fundamental concepts, key functions, identities, and applications demonstrate its significance in various fields, including physics, engineering, astronomy, and computer graphics. Understanding trigonometry involves recognizing the relationships between angles and sides, utilizing trigonometric ratios, and applying identities to solve problems. As we continue to explore the rich landscape of mathematics, the study of trigonometry will remain an essential area of research and application, inspiring curiosity and discovery in the realm of angles and measurements. Whether in theoretical mathematics or practical applications, trigonometry serves as a cornerstone for understanding the relationships between angles, distances, and real-world phenomena, making it an essential topic for anyone interested in mathematics.