Understanding the Unit of Electric Field: A Comprehensive Exploration

The electric field is a fundamental concept in electromagnetism, representing the influence that electric charges exert on one another. It is a vector field that describes the force experienced by a unit positive charge placed in the vicinity of other electric charges. Understanding the unit of electric field is crucial for grasping the principles of electricity and magnetism, as well as their applications in various fields such as physics, engineering, and technology. This article will provide an in-depth examination of the electric field, its definition, unit, characteristics, calculation methods, applications, and illustrative explanations to enhance understanding.

1. Definition of Electric Field

An electric field is defined as the region around a charged object where other charged objects experience a force. It is created by electric charges, and its strength and direction depend on the amount of charge and the distance from the charge. The electric field ( $\mathbf{E}$ ) at a point in space is defined as the force ( $\mathbf{F}$ ) experienced by a small positive test charge ( $q_0$ ) placed at that point, divided by the magnitude of the test charge:

$\mathbf{E} = \frac{\mathbf{F}}{q_0}$

Illustrative Explanation: Imagine a large magnet placed on a table. If you bring a small metal object (like a paperclip) close to the magnet, the paperclip will experience a force that pulls it toward the magnet. In this analogy, the area around the magnet where the paperclip feels this force represents the magnetic field. Similarly, the electric field is the area around a charged object where other charges feel a force.

2. Unit of Electric Field

The unit of electric field in the International System of Units (SI) is volts per meter (V/m). This unit can be understood as follows:

Volts (V): A volt is the unit of electric potential difference, which represents the amount of energy (in joules) per unit charge (in coulombs). It indicates how much work is done to move a charge between two points in an electric field.
Meters (m): A meter is the unit of distance in the SI system. In the context of electric fields, it represents the distance over which the electric force acts.

Thus, when we say that the electric field is measured in volts per meter, we are indicating how much electric potential (voltage) exists per unit distance in the field.

Illustrative Explanation: Think of the electric field as a hill. The height of the hill represents the electric potential (voltage), and the steepness of the hill represents the electric field strength. If you were to walk up the hill (move through the electric field), the height you gain (voltage) per step you take (distance) gives you the steepness of the hill, which is analogous to the electric field measured in volts per meter.

3. Characteristics of Electric Fields

Electric fields possess several key characteristics that are important for understanding their behavior:

Direction: The direction of the electric field is defined as the direction of the force that a positive test charge would experience. Electric fields point away from positive charges and toward negative charges.
Strength: The strength of the electric field is determined by the amount of charge creating the field and the distance from the charge. The electric field strength decreases with increasing distance from the charge.
Superposition Principle: The total electric field created by multiple charges is the vector sum of the electric fields produced by each charge individually. This principle allows us to calculate the electric field in complex systems.

Illustrative Explanation: Imagine a group of people at a concert, each holding a balloon. The balloons represent positive charges, and the people represent the electric field. If someone releases their balloon, it will float away from them (the direction of the electric field). If multiple people release their balloons, the balloons will spread out, and the overall pattern of balloons in the air represents the combined electric field from all the people.

4. Calculation of Electric Field

The electric field can be calculated using different methods depending on the configuration of the charges:

Point Charge: For a single point charge ( 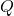$Q$ ), the electric field at a distance ( $r$ ) from the charge is given by Coulomb’s law:

$\mathbf{E} = \frac{k \cdot |Q|}{r^2}$

where $k$ is Coulomb’s constant ( $8.99 \times 10^9 \, \text{N m}^2/\text{C}^2$ ).

Uniform Electric Field: In a uniform electric field, such as that between two parallel plates, the electric field strength ( 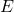$E$ ) can be calculated using the voltage ( 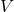$V$ ) across the plates and the distance ( 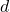$d$ ) between them:

$E = \frac{V}{d}$

Multiple Charges: For multiple point charges, the total electric field at a point is the vector sum of the electric fields due to each charge:

$\mathbf{E}_{\text{total}} = \mathbf{E}_1 + \mathbf{E}_2 + \mathbf{E}_3 + \ldots$

Illustrative Explanation: Consider a water fountain with multiple jets. Each jet represents a point charge creating its own water spray (electric field). If you want to know how much water is falling at a specific point in the fountain, you would need to consider the contributions from each jet (vector sum of electric fields). If the jets are all at the same height (uniform electric field), you can easily calculate the total water flow (electric field strength) based on the height of the fountain (voltage) and the distance from the base (distance between plates).

5. Applications of Electric Fields

Electric fields have numerous applications across various fields, including:

Electrostatics: Understanding electric fields is essential in electrostatics, where charges are at rest. This knowledge is applied in devices like capacitors, which store electric energy.
Electrical Engineering: Electric fields are fundamental in designing circuits, sensors, and other electronic components. Engineers use electric field principles to ensure devices operate efficiently and safely.
Medical Applications: Electric fields are used in medical devices such as electrocardiograms (ECGs) and defibrillators, which monitor and regulate heart activity.
Telecommunications: Electric fields play a crucial role in the transmission of signals in communication systems, including radio waves and fiber optics.

Illustrative Explanation: Imagine a city’s electrical grid as a network of roads (electric fields) that connect various buildings (devices). Just as the roads allow cars (electric current) to travel between buildings, electric fields enable the flow of electricity between components in a circuit. Understanding how these roads are laid out (electric field principles) is essential for ensuring that traffic flows smoothly and efficiently.

6. Conclusion

The unit of electric field is a fundamental concept in electromagnetism, providing a framework for understanding how electric charges interact with one another. By exploring its definition, unit, characteristics, calculation methods, applications, and illustrative explanations, we gain a deeper appreciation for the significance of electric fields in various scientific and engineering contexts. From electrostatics to telecommunications, the principles of electric fields are essential for designing and analyzing systems that rely on electric charge interactions. Understanding electric fields allows scientists and engineers to harness the power of electricity, contributing to advancements in technology and improving our daily lives. Whether you are studying the behavior of charged particles or designing complex electronic circuits, the concept of electric fields remains a cornerstone of modern physics and engineering.

Blog.Pengayaan.Com