In statistics, the Z-score is a powerful tool used to understand the position of a data point relative to the mean of a dataset. It quantifies how many standard deviations a data point is from the mean, allowing for comparisons across different datasets. The Z-score table, also known as the standard normal table, provides the probabilities associated with Z-scores in a standard normal distribution. This article will explore the concept of Z-scores, the construction and use of the Z-score table, and illustrative explanations to enhance understanding.
What is a Z-Score?
Definition of a Z-Score
A Z-score, or standard score, is calculated using the following formula:
![\[ Z = \frac{(X - \mu)}{\sigma} \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-4a179fcc5e2762fd33e5f6d48361ba28_l3.png "Rendered by QuickLaTeX.com")
Where:
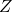= Z-score
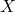= value of the data point
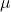= mean of the dataset
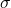= standard deviation of the dataset
The Z-score indicates how many standard deviations a particular value is from the mean . A positive Z-score indicates that the value is above the mean, while a negative Z-score indicates that it is below the mean.
Illustrative Explanation
Consider a dataset representing the heights of a group of individuals, with a mean height of 170 cm and a standard deviation of 10 cm. If an individual has a height of 180 cm, the Z-score can be calculated as follows:
![\[ Z = \frac{(180 - 170)}{10} = \frac{10}{10} = 1 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-2305c733e559b887f14c1d2edc8536e4_l3.png "Rendered by QuickLaTeX.com")
This Z-score of 1 indicates that the individual’s height is 1 standard deviation above the mean height of the group.
Understanding the Standard Normal Distribution
Definition
The standard normal distribution is a special case of the normal distribution where the mean is 0 and the standard deviation is 1. It is symmetric and bell-shaped, with the majority of the data points concentrated around the mean.
Properties of the Standard Normal Distribution
1. Symmetry: The distribution is symmetric about the mean (0).
2. Total Area: The total area under the curve is equal to 1.
3. Empirical Rule: Approximately 68% of the data falls within 1 standard deviation of the mean, about 95% falls within 2 standard deviations, and about 99.7% falls within 3 standard deviations.
Illustrative Explanation
Imagine a bell curve representing the heights of individuals in a population. The peak of the curve represents the mean height, while the spread of the curve indicates the standard deviation. The area under the curve represents the probability of finding individuals within certain height ranges.
The Z-Score Table
Definition
The Z-score table provides the cumulative probabilities associated with Z-scores in the standard normal distribution. It shows the area under the curve to the left of a given Z-score, which represents the probability of a value being less than or equal to that Z-score.
Structure of the Z-Score Table
The Z-score table is typically organized in a grid format, with the Z-scores listed along the rows and columns. The first two digits of the Z-score are found in the leftmost column, while the second decimal place is found in the top row. The intersection of the row and column gives the cumulative probability.
Example of a Z-Score Table
| Z | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.5000 | 0.5040 | 0.5080 | 0.5120 | 0.5160 | 0.5199 | 0.5239 | 0.5279 | 0.5319 | 0.5359 |
| 0.1 | 0.5398 | 0.5438 | 0.5478 | 0.5517 | 0.5557 | 0.5596 | 0.5636 | 0.5675 | 0.5714 | 0.5753 |
| 0.2 | 0.5793 | 0.5832 | 0.5871 | 0.5910 | 0.5948 | 0.5987 | 0.6026 | 0.6064 | 0.6103 | 0.6141 |
| 0.3 | 0.6179 | 0.6217 | 0.6255 | 0.6293 | 0.6331 | 0.6368 | 0.6406 | 0.6443 | 0.6480 | 0.6517 |
| 0.4 | 0.6554 | 0.6591 | 0.6628 | 0.6664 | 0.6700 | 0.6736 | 0.6772 | 0.6808 | 0.6844 | 0.6879 |
Using the Z-Score Table
To use the Z-score table, follow these steps:
1. Calculate the Z-Score: Use the Z-score formula to find the Z-score for the value of interest.
2. Locate the Z-Score in the Table: Find the Z-score in the leftmost column and the top row of the table.
3. Read the Probability: The intersection of the row and column will give you the cumulative probability associated with that Z-score.
Illustrative Example
Suppose you want to find the probability of a value being less than 175 cm in the earlier example where the mean height is 170 cm and the standard deviation is 10 cm.
1. Calculate the Z-Score:
![\[ Z = \frac{(175 - 170)}{10} = \frac{5}{10} = 0.5 \]](https://pengayaan.com/blog/wp-content/uploads/2024/12/quicklatex.com-eaa98d9916b3f8b0b23b5b02cb48b361_l3.png "Rendered by QuickLaTeX.com")
2. Locate the Z-Score in the Table: Find 0.5 in the left column and the corresponding cumulative probability in the table.
3. Read the Probability: The cumulative probability for a Z-score of 0.5 is approximately 0.6915. This means that about 69.15% of individuals in the population have a height less than 175 cm.
Applications of Z-Scores and Z-Score Tables
Z-scores and Z-score tables have numerous applications across various fields:
1. Standardization of Data
Z-scores allow for the standardization of data from different distributions, enabling comparisons across datasets. This is particularly useful in research and analysis.
2. Statistical Inference
Z-scores are used in hypothesis testing and confidence interval estimation. They help determine the likelihood of observing a sample mean under a null hypothesis.
3. Quality Control
In manufacturing and quality control, Z-scores are used to monitor processes and identify outliers. They help assess whether a process is operating within acceptable limits.
4. Finance
In finance, Z-scores are used to assess the risk of investments and to identify potential outliers in financial data. They help investors make informed decisions based on statistical analysis.
5. Psychometrics
In psychology and education, Z-scores are used to interpret standardized test scores. They help compare individual performance to the average performance of a group.
Conclusion
The Z-score is a vital statistical concept that quantifies the position of a data point relative to the mean of a dataset. The Z-score table provides cumulative probabilities associated with Z-scores in a standard normal distribution, making it a valuable tool for statistical analysis. By understanding how to calculate and interpret Z-scores and utilize the Z-score table, individuals can make informed decisions based on data, conduct hypothesis testing, and analyze various phenomena across different fields. As we continue to explore the world of statistics, the Z-score and its associated table will remain essential tools in our analytical toolkit, enabling us to navigate the complexities of data interpretation and decision-making effectively.