Cara Menghitung Hasil Pemangkatan

Pemangkatan adalah salah satu operasi matematika yang sering digunakan dalam berbagai konteks, baik dalam matematika dasar maupun dalam aplikasi yang lebih kompleks. Pemangkatan melibatkan pengalian suatu bilangan dengan dirinya sendiri sejumlah tertentu. Misalnya, jika kita memiliki bilangan $a$ dan kita ingin memangkatan bilangan tersebut dengan eksponen $n$ , maka kita menuliskannya sebagai $a^n$ . Dalam artikel ini, kita akan membahas secara mendetail tentang cara menghitung hasil pemangkatan, termasuk definisi, langkah-langkah, dan contoh-contoh yang relevan.

1. Pengertian Pemangkatan

a. Definisi Pemangkatan

Pemangkatan adalah operasi matematika yang melibatkan dua bilangan: basis dan eksponen. Basis adalah bilangan yang akan dipangkatkan, sedangkan eksponen menunjukkan berapa kali basis tersebut dikalikan dengan dirinya sendiri. Notasi pemangkatan dituliskan sebagai $a^n$ , di mana:

$a$ adalah basis.
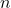$n$ adalah eksponen.

Sebagai contoh, $2^3$ berarti $2$ dikalikan dengan dirinya sendiri sebanyak 3 kali, yaitu $2 \times 2 \times 2 = 8$ .

b. Notasi Pemangkatan

Notasi pemangkatan dapat dituliskan dalam bentuk:

Basis: Bilangan yang akan dipangkatkan.
Eksponen: Angka yang menunjukkan berapa kali basis dikalikan dengan dirinya sendiri.

Contoh:

$5^2 = 5 \times 5 = 25$
$3^4 = 3 \times 3 \times 3 \times 3 = 81$

2. Langkah-langkah Menghitung Hasil Pemangkatan

a. Menentukan Basis dan Eksponen

Langkah pertama dalam menghitung hasil pemangkatan adalah menentukan basis dan eksponen. Misalnya, jika kita ingin menghitung $4^3$ :

Basis: $4$
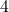
Eksponen: $3$

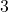
b. Mengalikan Basis dengan Diri Sendiri

Setelah menentukan basis dan eksponen, langkah selanjutnya adalah mengalikan basis dengan dirinya sendiri sesuai dengan nilai eksponen. Dalam contoh $4^3$ :

Kita mengalikan 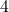$4$ sebanyak 3 kali:

– $4 \times 4 = 16$ (ini adalah hasil dari $4^2$ )
– Kemudian, kita kalikan hasil tersebut dengan $4$ lagi:
– $16 \times 4 = 64$

Jadi, $4^3 = 64$ .

c. Menggunakan Notasi Pemangkatan untuk Bilangan Negatif dan Nol

Pemangkatan juga dapat diterapkan pada bilangan negatif dan nol. Berikut adalah beberapa aturan yang perlu diingat:

Bilangan Negatif: Jika basis adalah bilangan negatif, hasil pemangkatan akan tergantung pada eksponen:

– Jika eksponen genap, hasilnya positif. Contoh: $(-2)^2 = 4$
– Jika eksponen ganjil, hasilnya negatif. Contoh: $(-2)^3 = -8$

Nol: Pemangkatan nol memiliki aturan khusus:

– $0^n = 0$ untuk semua $n > 0$
– $0^0$ adalah bentuk yang tidak terdefinisi dalam banyak konteks, tetapi sering dianggap sebagai 1 dalam beberapa bidang matematika.

d. Menggunakan Kalkulator atau Software

Untuk bilangan yang lebih besar atau eksponen yang lebih tinggi, menghitung pemangkatan secara manual bisa menjadi rumit. Dalam kasus ini, kita dapat menggunakan kalkulator atau perangkat lunak matematika. Sebagian besar kalkulator ilmiah memiliki tombol pemangkatan (biasanya ditandai dengan $x^y$ atau $a^b$ ) yang memungkinkan kita untuk memasukkan basis dan eksponen dengan mudah.

3. Contoh Penghitungan Pemangkatan

a. Contoh 1: Menghitung 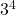$3^4$

1. Menentukan basis dan eksponen:
– Basis: $3$
– Eksponen: $4$

2. Mengalikan basis dengan dirinya sendiri:
– $3 \times 3 = 9$ (ini adalah $3^2$ )
– $9 \times 3 = 27$ (ini adalah $3^3$ )
– $27 \times 3 = 81$

Jadi, $3^4 = 81$ .

b. Contoh 2: Menghitung 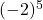$(-2)^5$

1. Menentukan basis dan eksponen:
– Basis: $-2$
– Eksponen: $5$

2. Mengalikan basis dengan dirinya sendiri:
– $-2 \times -2 = 4$ (ini adalah $(-2)^2$ )
– $4 \times -2 = -8$ (ini adalah $(-2)^3$ )
– $-8 \times -2 = 16$ (ini adalah $(-2)^4$ )
– $16 \times -2 = -32$

Jadi, $(-2)^5 = -32$ .

c. Contoh 3: Menghitung 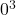$0^3$

1. Menentukan basis dan eksponen:
– Basis: $0$
– Eksponen: $3$

2. Menggunakan aturan pemangkatan:
– $0^3 = 0$

Jadi, $0^3 = 0$ .

4. Kesimpulan

Menghitung hasil pemangkatan adalah proses yang melibatkan pengalian bilangan dengan dirinya sendiri sesuai dengan nilai eksponen. Dengan memahami langkah-langkah dasar dalam pemangkatan, kita dapat menghitung hasil pemangkatan dengan lebih mudah, baik secara manual maupun menggunakan alat bantu seperti kalkulator. Pemangkatan memiliki banyak aplikasi dalam matematika, fisika, dan ilmu lainnya, sehingga penting untuk menguasai konsep ini. Dengan latihan dan pemahaman yang baik, kita dapat dengan percaya diri menghitung hasil pemangkatan dalam berbagai konteks.

Pengayaan.com