Tabung adalah salah satu bentuk geometri tiga dimensi yang memiliki dua alas berbentuk lingkaran dan sisi tegak berbentuk persegi panjang. Dalam matematika, menghitung luas tabung melibatkan dua komponen utama: luas permukaan alas dan luas permukaan samping. Dalam artikel ini, kita akan membahas secara mendetail tentang cara menghitung luas tabung, termasuk rumus yang digunakan, langkah-langkah perhitungan, serta penjelasan ilustratif untuk setiap konsep.
1. Pengertian Tabung
Tabung adalah bangun ruang yang dibatasi oleh dua lingkaran sejajar (alas dan tutup) dan sebuah permukaan tegak yang melingkupi kedua lingkaran tersebut. Tabung memiliki dua jari-jari (r) yang sama pada alas dan tutup, serta tinggi (h) yang merupakan jarak antara kedua alas tersebut.
Ilustrasi Konsep
Bayangkan tabung sebagai sebuah kaleng minuman. Alas dan tutup kaleng adalah dua lingkaran, sementara sisi kaleng adalah permukaan tegak yang menghubungkan kedua alas tersebut. Ketika kita menghitung luas tabung, kita akan menghitung luas kaleng tersebut secara keseluruhan.
2. Rumus Menghitung Luas Tabung
Luas permukaan tabung terdiri dari dua bagian:
1. Luas Permukaan Alas: Luas dari salah satu lingkaran (alas).
2. Luas Permukaan Samping: Luas dari permukaan tegak yang mengelilingi tabung.
Rumus untuk menghitung luas permukaan tabung adalah sebagai berikut:
![[ text{Luas Permukaan Tabung} = 2 times text{Luas Alas} + text{Luas Permukaan Samping} ]](https://pengayaan.com/wp-content/uploads/2025/07/img_6875a690d0cad.png "Rendered by QuickLaTeX.com")
Di mana:
- Luas Alas =
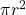(dengan 
adalah jari-jari lingkaran) - Luas Permukaan Samping =
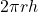(dengan 
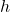adalah tinggi tabung)
Sehingga, rumus lengkapnya menjadi:
![[ text{Luas Permukaan Tabung} = 2 pi r^2 + 2 pi r h ]](https://pengayaan.com/wp-content/uploads/2025/07/img_6875a69163658.png "Rendered by QuickLaTeX.com")
Ilustrasi Konsep
Bayangkan kita ingin mengecat kaleng minuman. Untuk mengetahui berapa banyak cat yang dibutuhkan, kita perlu menghitung luas permukaan kaleng tersebut. Luas permukaan terdiri dari dua bagian: bagian atas dan bawah (alas) serta bagian samping (permukaan tegak). Kita akan menghitung luas masing-masing bagian dan menjumlahkannya untuk mendapatkan total luas yang perlu dicat.
3. Langkah-langkah Menghitung Luas Tabung
Mari kita lakukan langkah-langkah untuk menghitung luas tabung dengan contoh konkret.
Contoh Soal
Misalkan kita memiliki tabung dengan jari-jari 
cm dan tinggi 
cm. Kita akan menghitung luas permukaan tabung tersebut.
Langkah 1: Hitung Luas Alas
Gunakan rumus luas alas:
![[ text{Luas Alas} = pi r^2 ]](https://pengayaan.com/wp-content/uploads/2025/07/img_6875a6919ca3a.png "Rendered by QuickLaTeX.com")
Substitusi nilai :
![[ text{Luas Alas} = pi (3 text{ cm})^2 = pi times 9 text{ cm}^2 approx 28.27 text{ cm}^2 ]](https://pengayaan.com/wp-content/uploads/2025/07/img_6875a691adefd.png "Rendered by QuickLaTeX.com")
Ilustrasi Konsep
Bayangkan kita menggambar lingkaran dengan jari-jari 3 cm. Luas lingkaran ini adalah area yang akan kita cat di bagian atas dan bawah tabung.
Langkah 2: Hitung Luas Permukaan Samping
Gunakan rumus luas permukaan samping:
![[ text{Luas Permukaan Samping} = 2 pi r h ]](https://pengayaan.com/wp-content/uploads/2025/07/img_6875a691c4a06.png "Rendered by QuickLaTeX.com")
Substitusi nilai dan :
![[ text{Luas Permukaan Samping} = 2 pi (3 text{ cm})(5 text{ cm}) = 30pi text{ cm}^2 approx 94.25 text{ cm}^2 ]](https://pengayaan.com/wp-content/uploads/2025/07/img_6875a691db31e.png "Rendered by QuickLaTeX.com")
Ilustrasi Konsep
Bayangkan kita membuka kaleng minuman dan mengukur permukaan bagian sampingnya. Luas permukaan samping adalah area yang akan kita cat di sisi kaleng.
Langkah 3: Hitung Total Luas Permukaan Tabung
Sekarang kita dapat menghitung total luas permukaan tabung dengan menjumlahkan luas alas dan luas permukaan samping:
Substitusi nilai yang telah kita hitung:
![[ text{Luas Permukaan Tabung} = 2 times 28.27 text{ cm}^2 + 94.25 text{ cm}^2 ]](https://pengayaan.com/wp-content/uploads/2025/07/img_6875a691ef61f.png "Rendered by QuickLaTeX.com")
![[ text{Luas Permukaan Tabung} approx 56.54 text{ cm}^2 + 94.25 text{ cm}^2 approx 150.79 text{ cm}^2 ]](https://pengayaan.com/wp-content/uploads/2025/07/img_6875a69213abb.png "Rendered by QuickLaTeX.com")
4. Kesimpulan
Menghitung luas tabung melibatkan pemahaman tentang rumus luas alas dan luas permukaan samping. Dengan mengikuti langkah-langkah yang telah dijelaskan, kita dapat dengan mudah menghitung luas permukaan tabung untuk berbagai ukuran. Luas permukaan tabung sangat penting dalam berbagai aplikasi, seperti dalam industri kemasan, konstruksi, dan desain produk. Mari kita terus berlatih dan menerapkan konsep ini dalam kehidupan sehari-hari untuk meningkatkan pemahaman kita tentang geometri!