Geometri analitis adalah cabang matematika yang memadukan aljabar dan geometri menggunakan sistem koordinat. Artikel ini mengulas konsep-konsep penting seperti titik, garis, lingkaran, dan parabola, dilengkapi contoh ilustratif nyata untuk setiap konsep.
Geometri analitis, juga dikenal sebagai geometri koordinat, adalah cabang matematika yang menggabungkan prinsip-prinsip aljabar dengan geometri. Dengan menggunakan sistem koordinat kartesius, konsep-konsep geometri yang dulunya hanya divisualisasikan kini bisa dihitung dan dianalisis secara numerik. Hal ini menjadikan geometri analitis sebagai alat penting tidak hanya dalam matematika murni, tetapi juga dalam fisika, teknik, arsitektur, bahkan ekonomi.
Dalam artikel ini, kita akan membahas secara mendalam beberapa konsep utama dalam geometri analitis, seperti titik, garis, jarak, kemiringan, hingga bentuk kurva seperti lingkaran dan parabola. Setiap bagian dilengkapi contoh nyata agar lebih mudah dipahami dan diaplikasikan.
Geometri analitik memungkinkan persamaan matematika direpresentasikan secara grafis. Geometri analitis adalah cabang matematika yang menggabungkan konsep geometri dan aljabar. Dalam geometri analitis, titik dalam ruang dua dimensi atau tiga dimensi direpresentasikan dengan koordinat, sehingga memungkinkan untuk memecahkan masalah geometri menggunakan metode aljabar. Geometri analitis memungkinkan kita untuk memahami hubungan antara bentuk geometris dengan persamaan matematika.
Apa itu geometri analitik?
Geometri analitik adalah cabang matematika yang didedikasikan untuk studi mendalam tentang bangun-bangun geometri dan datanya masing-masing, seperti luas, jarak, volume, titik potong, sudut kemiringan, dll. Untuk melakukan hal ini, menggunakan teknik dasar analisis matematika dan aljabar.
Ia menggunakan sistem koordinat yang dikenal sebagai Bidang Kartesius, yang berbentuk dua dimensi dan terdiri dari dua sumbu: satu absis (sumbu x) dan sumbu ordinat lainnya (sumbu y). Di sana kita dapat mempelajari semua bangun geometri yang menarik bagi kita, dengan menetapkan setiap titik pada bangun tersebut lokasi koordinat tertentu (x, y).
Dengan demikian, analisis geometri analitik biasanya mencakup interpretasi matematis suatu bangun geometri, yaitu perumusan persamaan. Atau bisa juga sebaliknya: representasi grafis dari persamaan matematika. Kesetaraan ini dinyatakan dalam rumus y = f(x), di mana f adalah suatu fungsi bertipe tertentu.
Geometri analitik adalah bidang dasar matematika yang biasanya menjadi bagian dari kurikulum sekolah menengah.
Lihat juga: Fungsi matematika
Sejarah geometri analitik
Pendiri bidang studi ini dianggap filsuf Perancis René Descartes (1596-1650), dengan lampiran berjudul “ La Geometrie ” dalam karyanya yang terkenal Discourse on Method .
Namun, pada abad ke-11, matematikawan Persia Omar Khayyam (c.1048-c.1131) menggunakan gagasan serupa, yang hampir tidak mungkin diketahui oleh Descartes. Artinya, keduanya mungkin menciptakannya sendiri.
Mengingat sifat hermetis dari gagasan Descartes, matematikawan Belanda Franz van Schooten (1615-1660) dan kolaboratornya memperluas, mengembangkan, dan menyebarkan geometri analitik di Barat. Dulu disebut “Geometri Cartesian,” untuk memberi penghormatan kepada penciptanya, namun istilah tersebut saat ini lebih suka digunakan untuk merujuk hanya pada lampiran yang ditulis oleh Descartes.
Titik dan Sistem Koordinat
Dasar dari geometri analitis adalah sistem koordinat kartesius, di mana setiap titik dalam bidang datar diwakili oleh sepasang bilangan 
.
Contoh Ilustratif:
Bayangkan sebuah papan tulis yang dibagi menjadi empat bagian oleh dua garis lurus saling tegak lurus: garis horizontal (sumbu-X) dan garis vertikal (sumbu-Y). Titik pusat pertemuan keduanya disebut titik asal (0,0).
Misalnya, titik A dengan koordinat (3, 4) berarti 3 satuan ke kanan dari titik asal, dan 4 satuan ke atas. Jika Andi berdiri di titik (0,0) dan melangkah ke titik (3,4), maka ia bergerak ke arah timur laut.
Penerapan geometri analitik
Jembatan gantung dapat dirancang berkat geometri analitik.
Geometri analitik adalah salah satu alat konseptual yang paling berguna bagi umat manusia, dan saat ini kita dapat melihat penerapannya, misalnya saja:
- Jembatan gantung. Dari jembatan gantung kayu tua hingga versi modern dengan kabel baja, prinsip geometris parabola diterapkan di masing-masing jembatan.
- Piringan satelit. Antena parabola untuk menangkap informasi satelit berbentuk paraboloid, dihasilkan oleh reflektornya yang berputar pada porosnya mengejar sinyal. Berkat sifat refleksi parabola, parabola dapat memantulkan sinyal satelit ke perangkat pemberi makan.
- Pengamatan astronomi. Benda langit mengorbit dalam jalur yang menggambarkan elips, seperti yang disimpulkan oleh Johannes Kepler (1571-1630), dan bukan lingkaran, seperti yang diyakini Copernicus (1473-1543). Perhitungan ini hanya mungkin dilakukan dengan menggunakan Geometri analitik.
Rumus geometri analitik
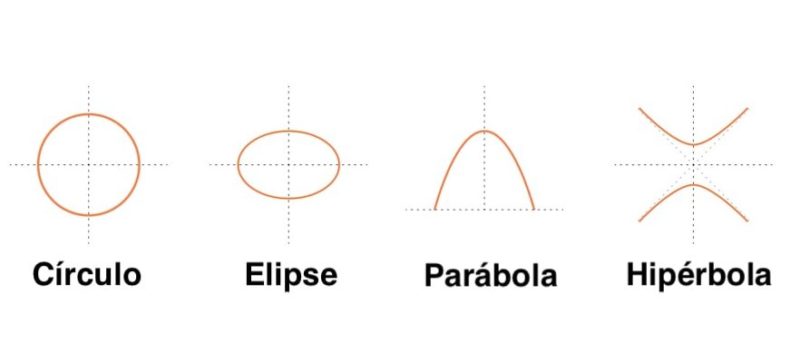
Geometri analitik menawarkan rumus untuk bangun geometri.
Geometri mempelajari bangun-bangun geometri dan memperoleh persamaan dasarnya, seperti:
- Garis lurus digambarkan dengan rumus ax + by = c .
- Lingkaran digambarkan dengan rumus x 2 + y 2 = 4 .
- Hiperbola digambarkan dengan rumus xy = 1 .
- Parabola digambarkan dengan rumus y = ax 2 + bx + c .
- Elips dijelaskan dengan rumus (x 2 /a 2 ) + (y 2 /b 2 ) = 1 .
Jarak Antara Dua Titik
Salah satu aplikasi awal dalam geometri analitis adalah menghitung jarak antara dua titik dengan menggunakan rumus Pythagoras dalam sistem koordinat.
Rumus:
Jika titik A 
dan titik B 
, maka:
![\[\text{Jarak AB} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\]](https://pengayaan.com/wp-content/uploads/2025/07/3_geometri-analitis.png "Rendered by QuickLaTeX.com")
Contoh Ilustratif:
Titik A (2, 3) dan titik B (7, 11).
Maka jaraknya adalah:
![\[\sqrt{(7 - 2)^2 + (11 - 3)^2} = \sqrt{25 + 64} = \sqrt{89} \approx 9,43 \text{ satuan}\]](https://pengayaan.com/wp-content/uploads/2025/07/4_geometri-analitis.png "Rendered by QuickLaTeX.com")
Jika titik A adalah rumah Rina dan titik B adalah sekolahnya, maka jarak lurus antara rumah dan sekolah adalah sekitar 9,43 satuan (misalnya kilometer).
Gradien dan Persamaan Garis Lurus
Gradien (kemiringan) suatu garis mengukur seberapa curam garis itu naik atau turun. Dalam geometri analitis, gradien antara dua titik dinyatakan sebagai:
![\[m = \frac{y_2 - y_1}{x_2 - x_1}\]](https://pengayaan.com/wp-content/uploads/2025/07/5_geometri-analitis.png "Rendered by QuickLaTeX.com")
Persamaan garis umum yang melewati titik dengan gradien tertentu adalah:
![\[y = mx + c\]](https://pengayaan.com/wp-content/uploads/2025/07/6_geometri-analitis.png "Rendered by QuickLaTeX.com")
Contoh Ilustratif:
Diketahui dua titik: P (1, 2) dan Q (4, 8).
Gradien garis PQ adalah:
![\[m = \frac{8 - 2}{4 - 1} = \frac{6}{3} = 2\]](https://pengayaan.com/wp-content/uploads/2025/07/7_geometri-analitis.png "Rendered by QuickLaTeX.com")
Substitusi ke dalam persamaan 
dengan menggunakan titik P (1,2):
![\[2 = 2(1) + c \Rightarrow c = 0\]](https://pengayaan.com/wp-content/uploads/2025/07/9_geometri-analitis.png "Rendered by QuickLaTeX.com")
Maka, persamaan garisnya:
![\[y = 2x\]](https://pengayaan.com/wp-content/uploads/2025/07/10_geometri-analitis.png "Rendered by QuickLaTeX.com")
Jika garis ini mewakili lintasan air yang mengalir dari tangki ke selokan, maka air mengalir turun dua satuan secara vertikal untuk setiap satuan pergeseran horizontal ke kanan.
Persamaan Lingkaran
Dalam sistem koordinat, sebuah lingkaran dengan pusat di 
dan jari-jari 
memiliki persamaan:
![\[(x - h)^2 + (y - k)^2 = r^2\]](https://pengayaan.com/wp-content/uploads/2025/07/13_geometri-analitis.png "Rendered by QuickLaTeX.com")
Contoh Ilustratif:
Sebuah kolam berbentuk bundar memiliki pusat di titik (5,5) dan jari-jari 4 meter. Maka persamaan lingkarannya adalah:
![\[(x - 5)^2 + (y - 5)^2 = 16\]](https://pengayaan.com/wp-content/uploads/2025/07/14_geometri-analitis.png "Rendered by QuickLaTeX.com")
Jika Dina ingin menggambar batas kolam di software desain lanskap, ia bisa menggunakan persamaan ini untuk memastikan bentuknya benar-benar simetris dan proporsional.
Parabola: Kurva Simetris dengan Aplikasi Luas
Parabola adalah kurva berbentuk “U” atau “∩” yang dapat dibentuk oleh lintasan objek yang dilempar, reflektor satelit, atau bahkan jembatan gantung. Bentuk umumnya:
![\[y = ax^2 + bx + c\]](https://pengayaan.com/wp-content/uploads/2025/07/15_geometri-analitis.png "Rendered by QuickLaTeX.com")
Jika 
, parabola terbuka ke atas; jika 
, terbuka ke bawah.
Contoh Ilustratif:
Sebuah bola dilempar ke udara, dan lintasannya dapat dijelaskan oleh persamaan:
![\[y = -x^2 + 6x\]](https://pengayaan.com/wp-content/uploads/2025/07/18_geometri-analitis.png "Rendered by QuickLaTeX.com")
Ini menunjukkan bahwa ketinggian bola (
) tergantung pada posisi horizontal (
). Titik tertinggi bola terjadi saat 
, dengan ketinggian 
. Maka bola mencapai puncak lintasan pada titik (3,9).
Aplikasi Geometri Analitis dalam Kehidupan
Geometri analitis tidak hanya dipelajari di ruang kelas, tetapi juga digunakan secara luas dalam kehidupan nyata. Dari arsitek yang mendesain gedung, insinyur yang membuat jembatan, hingga programmer yang mengembangkan game berbasis grafis — semuanya bergantung pada prinsip-prinsip geometri analitis.
Contoh Ilustratif:
Sebuah insinyur sipil ingin menentukan titik tertinggi dari jembatan gantung agar struktur kabel simetris dan kuat. Ia menggunakan persamaan parabola untuk menentukan tinggi optimal dan lokasi penempatan pilar pendukung. Tanpa geometri analitis, penghitungan tersebut akan lebih rumit dan rawan kesalahan.
Kesimpulan
Geometri analitis menjembatani dunia geometri yang bersifat visual dengan kekuatan aljabar yang bersifat simbolik. Dengan memanfaatkan sistem koordinat, konsep seperti garis, kurva, dan bentuk dua dimensi bisa dijelaskan secara matematis dan terukur.
Setiap titik yang kita lihat di layar komputer, setiap garis pada peta digital, hingga setiap gerakan peluru dalam simulasi fisika, semuanya berakar pada geometri analitis. Pemahaman tentang bidang ini memberikan kita kekuatan untuk menggambarkan, menghitung, dan memprediksi fenomena ruang secara presisi — menjadikannya salah satu alat paling vital dalam ilmu pengetahuan dan teknologi modern.