Relevant Data:
- Sisi: Segitiga memiliki tiga sisi yang menghubungkan tiga titik sudutnya.
- Sudut: Segitiga memiliki tiga sudut dalam jumlah total 180 derajat.
- Jenis: Berdasarkan panjang sisi dan besaran sudutnya, segitiga dapat diklasifikasikan ke dalam berbagai jenis, seperti segitiga sama sisi, sama kaki, lancip, tumpul, atau siku-siku.
- Teorema Pythagoras: Teorema yang menghubungkan sisi-sisi segitiga siku-siku.
- Rumus: Berbagai rumus dalam segitiga, seperti rumus luas, rumus keliling, dan rumus trigonometri, digunakan untuk menghitung berbagai parameter segitiga.
Explanation:
Segitiga adalah bangun datar yang terdiri dari tiga sisi dan tiga sudut. Dalam geometri, segitiga memiliki peran penting karena merupakan struktur dasar yang digunakan dalam berbagai aplikasi matematika dan ilmu lainnya. Sifat-sifat segitiga, seperti jumlah total sudutnya 180 derajat, menjadikannya objek kajian yang menarik.
Dengan memahami sifat-sifat segitiga, kita dapat menghitung luas, keliling, dan berbagai parameter lainnya yang terkait dengan segitiga. Teorema Pythagoras, yang merupakan salah satu teorema penting dalam matematika, digunakan khususnya dalam segitiga siku-siku untuk menghubungkan panjang sisi-sisinya.
Klasifikasi segitiga berdasarkan sifat-sifatnya, seperti segitiga sama sisi, sama kaki, atau berdasarkan sudutnya, memberikan pemahaman yang lebih dalam tentang struktur segitiga. Rumus-rumus yang terkait dengan segitiga, seperti rumus luas, rumus keliling, dan rumus trigonometri, memainkan peran penting dalam pemecahan masalah geometri yang melibatkan segitiga.
Pemahaman yang baik tentang segitiga penting dalam berbagai bidang, seperti ilmu matematika, fisika, arsitektur, dan teknik. Segitiga menjadi landasan bagi pemahaman geometri yang lebih kompleks dan aplikasi praktis dalam kehidupan sehari-hari.
Resources:
- Buku: “Geometri Segitiga: Teori dan Aplikasi” oleh Prof. Dr. I Made Surya.
- Jurnal: “Penggunaan Segitiga dalam Konstruksi Bangunan” oleh Dr. Putri Wulandari.
- Website: www.segitiga-geometri.org – Sumber informasi dan tutorial mengenai segitiga dan aplikasinya dalam matematika dan ilmu terkait.
Apa itu segitiga?
Segitiga atau tritunggal adalah bangun datar geometri dasar yang mempunyai tiga sisi yang bersentuhan satu sama lain pada titik-titik yang sama yang disebut simpul. Namanya berasal dari fakta bahwa ia memiliki tiga sudut dalam atau dalam, yang dibentuk oleh setiap pasangan garis yang bersentuhan pada titik sudut yang sama.
Bentuk-bentuk geometris ini diberi nama dan diklasifikasikan menurut bentuk sisi-sisinya dan jenis sudut yang dibuatnya. Namun, sisi-sisinya selalu tiga dan jumlah semua sudutnya selalu 180°.
Segitiga telah dipelajari oleh umat manusia sejak dahulu kala, karena dikaitkan dengan ketuhanan, misteri, dan keajaiban. Oleh karena itu, mereka dapat ditemukan dalam banyak simbol okultisme (Freemasonry, ilmu sihir, Kabbalah, dll.) dan dalam tradisi keagamaan. Angka terkaitnya, tiga (3), secara numerologis menyinggung misteri pembuahan dan kehidupan itu sendiri.
Dalam sejarah segitiga, zaman kuno Yunani layak mendapat tempat yang menonjol. Pythagoras Yunani (c. 569 – c. 475 SM) mengajukan teorema terkenalnya untuk segitiga siku-siku, yang menyatakan bahwa kuadrat sisi miring sama dengan jumlah kuadrat kaki-kakinya.
Lihat juga: Trigonometri
Properti segitiga
Sifat segitiga yang paling jelas adalah ketiga sisinya, tiga titik sudutnya, dan tiga sudutnya, yang mungkin sama atau berbeda sama sekali satu sama lain. Segitiga adalah poligon paling sederhana yang pernah ada dan tidak memiliki diagonal, karena dengan tiga titik yang tidak sejajar, segitiga dapat dibentuk.
Faktanya, poligon lain dapat dibagi menjadi sekumpulan segitiga terurut, yang dikenal sebagai triangulasi , sehingga studi tentang segitiga merupakan hal mendasar dalam geometri.
Selain itu, segitiga selalu cembung, tidak pernah cekung, karena sudutnya tidak pernah melebihi 180° (atau π radian).
elemen segitiga
Segitiga terdiri dari tiga sisi yang bertemu pada tiga titik sudut.
Segitiga terdiri dari beberapa elemen, banyak di antaranya telah kami sebutkan:
- Sudut. Titik-titik inilah yang membentuk suatu segitiga dengan menghubungkan dua titik di antaranya dengan sebuah garis lurus. Jadi, jika kita mempunyai titik A, B, dan C, menghubungkannya dengan garis AB, BC, dan CA akan menghasilkan sebuah segitiga. Selanjutnya, simpul-simpul tersebut berada pada sisi berlawanan dari sudut dalam poligon.
- Sisi. Ini adalah nama yang diberikan untuk setiap garis yang menghubungkan titik sudut suatu segitiga, yang membatasi bangun (bagian dalam dari luar).
- Sudut. Masing-masing dua sisi segitiga membentuk suatu jenis sudut pada titik sudut yang sama, yang disebut sudut dalam, karena menghadap bagian dalam poligon. Sudut-sudut ini, seperti sisi dan simpul, selalu tiga.
Jenis-jenis segitiga
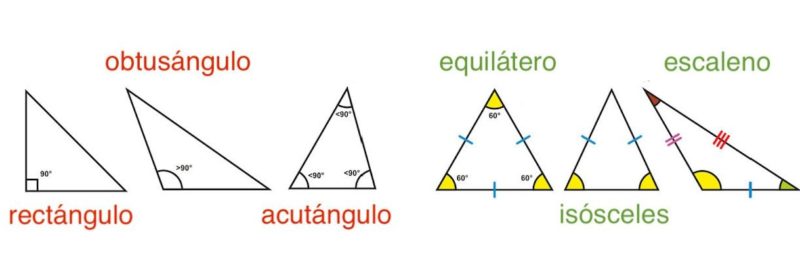
Segitiga dapat digolongkan berdasarkan sudutnya atau berdasarkan sisinya.
Ada dua klasifikasi utama segitiga:
- Menurut sisi-sisinya. Berdasarkan hubungan antara ketiga sisinya yang berbeda, suatu segitiga dapat berupa:
- Sama sisi. Jika ketiga sisinya mempunyai panjang yang sama persis.
- Sama kaki. Jika dua sisinya sama panjang dan sisi ketiga berbeda panjang.
- Sisi tak sama panjang. Apabila ketiga sisinya mempunyai panjang yang berbeda satu sama lain.
- Menurut sudutnya. Bergantung pada pembukaan sudutnya, kita dapat berbicara tentang segitiga:
- Persegi panjang. Mereka menyajikan sudut siku-siku (90°) yang terdiri dari dua sisi yang serupa (kaki) dan berlawanan dengan sisi ketiga (sisi miring).
- Sudut miring. Yang tidak menunjukkan sudut siku-siku, dan yang pada gilirannya dapat berupa:
- Sudut tumpul. Jika salah satu sudut dalamnya tumpul (lebih besar dari 90°) dan dua sudut lainnya lancip (kurang dari 90°).
- sudut tajam. Jika ketiga sudut dalamnya lancip (kurang dari 90°).
Kedua klasifikasi ini dapat digabungkan, memungkinkan kita berbicara tentang segitiga siku-siku sama kaki, segitiga lancip tak sama panjang, dll.
Keliling suatu segitiga
Keliling suatu segitiga dihitung dengan menjumlahkan sisi-sisinya.
Keliling suatu segitiga adalah jumlah panjang sisi-sisinya, dan biasanya dilambangkan dengan huruf p atau 2s . Persamaan untuk menentukan keliling segitiga ABC adalah:
p = AB + BC + CA.
Contoh: sebuah segitiga yang panjang sisinya 5cm, 5cm, dan 10cm mempunyai keliling 20cm.
Luas segitiga
Untuk menghitung luas segitiga perlu diketahui tingginya.
Luas segitiga (a) adalah ruang dalam yang dibatasi oleh ketiga sisinya. Dapat dihitung dengan mengetahui alasnya (b) dan tingginya (h), sesuai dengan rumus:
a = (bh)/2.
Luas diukur dalam satuan panjang kuadrat (cm 2 , m 2 , km 2 , dst.)
Alas segitiga adalah sisi di mana gambar tersebut “bertumpu”, biasanya sisi yang lebih rendah. Sebaliknya, untuk mencari tinggi suatu segitiga, kita perlu menarik garis dari titik sudut yang berhadapan dengan alasnya, yaitu sudut atas. Garis itu harus membentuk sudut siku-siku dengan alasnya.
Jadi, misalnya mempunyai segitiga sama kaki dengan panjang sisi: 11 cm, 11 cm, dan 7,5 cm, kita dapat menghitung tingginya (7 cm) lalu menerapkan rumus: a = (11 cm x 7 cm) / 2, yang menghasilkan hasil 38,5 cm 2 .
Angka geometris lainnya
Sosok geometris dua dimensi penting lainnya adalah:
- Kotak itu. Poligon dengan empat sisi yang sama sempurna, pendahulu kubus dua dimensi.
- Persegi panjang. Jika kita mengambil sebuah persegi dan memanjangkan dua sisi yang berhadapan, kita akan memperoleh bangun datar yang terdiri dari empat garis: dua sama besar dan dua berbeda (tetapi sama besar). Itu persegi panjang.
- Lingkaran. Kita semua mengetahui lingkaran, salah satu bentuk paling sederhana dalam geometri dan terdiri dari garis lengkung kontinu yang kembali ke titik awal dengan menelusuri keliling 360°.
Lanjutkan dengan: Matematika
Referensi
- “Segitiga” di Wikipedia.
- “Jenis-jenis segitiga (menurut sisi-sisinya dan sudut-sudutnya)” (video) di Academia Play.
- “Segitiga” di Instituto Monterrey.
- “Bagian-bagian dan sifat-sifat khusus segitiga” di Khan Academy.
- “Apa saja jenis-jenis segitiga?” di BBC Bitesize.
- “Segitiga (matematika)” dalam The Encyclopaedia Britannica.
